Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 3
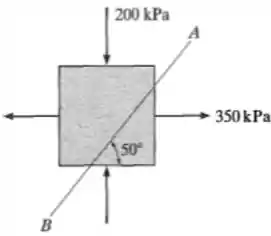
3. O estado de tensão em um ponto em um elemento estrutural é mostrado no elemento. Determine as componentes de tensão que agem no plano inclinado . Resolva o problema usando o método do equilíbrio descrito na Seção .
Passo 1
E aí meus queridos, tudo certinho?! Bora pra nossa questão sobre análise de tensões e deformações!
Se liga só! O segredo que o produtor vai passar aqui é infalível pra se resolver essa questão.
Tá ligado a linha ! Pois bem! Ela corta a seção transversal do nosso elemento plano, formando duas figuras geométricas, que são um triângulo com ângulo de com a horizontal e um outro polígono de lados. Este último, nós vamos ignorar totalmente. Afinal, tempo é ouro, né não?
Passo 2
Então vamos começar!
Duas tensões que estão atuando no nosso plano inclinado já tiramos de cara, que são:
1) a tensão na horizontal de
2) a tensão na vertical de .
E tem também outras duas tensões que estão implícitas aí... No caso, a força de tensão normal (perpendicular à superfície do elemento ) e a força de tensão cisalhante (paralela à superfície do elemento ).
O nosso ângulo pra análise já temos... A figura do enunciado foi gentil com a gente e já nos mostrou seu valor, que é de .
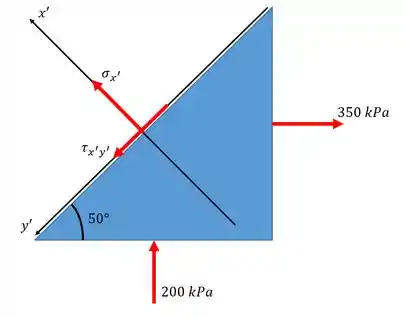
Sendo assim, com essas informações, chegamos até a seguinte figura abaixo...
Passo 3
Se antes estávamos nas direções e ; agora nos concentramos apenas nas direções e .
Veja bem! Chamemos de a área da face oblíqua do plano inclinado
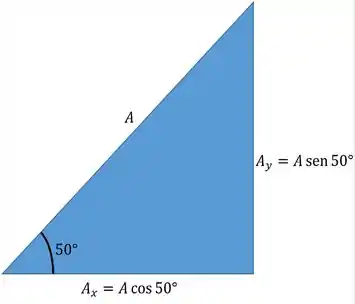
Essa face oblíqua está, assim como nosso triângulo inclinada de em relação a horizontal. Isso significa que ela pode ser decompostas tanto na direção horizontal quanto na direção vertical do seguinte jeito...
E como força nada mais é do que o produto da tensão pela área.
Então a gente pode representar nosso triângulo por forças ao invés de tensões, onde:
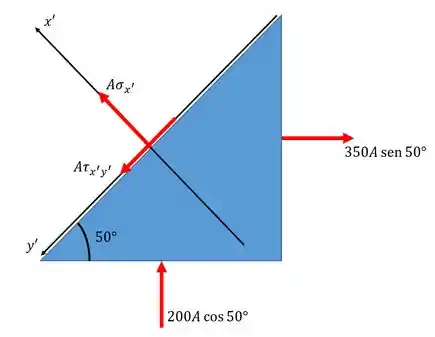
Passo 4
Pronto! A parte mais chatinha já foi!
O que nos resta fazer então, é aplicar o somatório das forças nas duas novas direções que temos para assim, obter nossas respostas...
Mas pra ficar ainda mais fácil, bora fazer um esboço dessa vez, só com as forças do nosso sistema...
Agora sim! Podemos identificar perfeitamente as forças em cada direção!
Então bora pro que interessa!
Primeiro o somatório em :
Sim, aqui os termos de seno e cosseno aparecem duas vezes mesmo porque um é relativo à decomposição da área e outro à decomposição da força =)
Já achamos o valor da tensão normal! Isso aí Estamos mandando bem!
Seguindo em frente... Pra encontrar a tensão cisalhante, dessa vez basta fazer o somatório das forças em :
Novamente os termos do cosseno e seno aparecem mais de uma vez mesmo porque a gente decompôs a força e a área.
E pronto! Finalizamos aqui!