Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 6
Um esquiador parte do repouso sobre uma encosta com no instante de tempo e registra o tempo quando passa um ponto de controle da velocidade metros abaixo na encosta. Determine o coeficiente de atrito dinâmico entre a neve e os esquis. Despreze a resistência do vento.
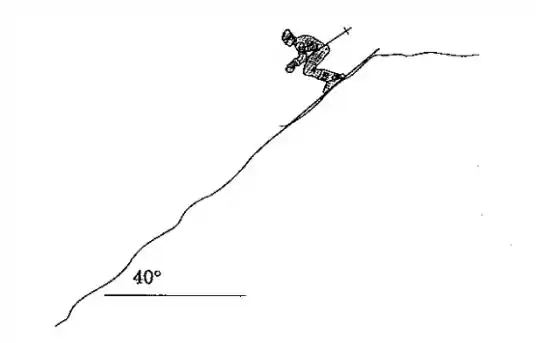
Passo 1
A informação mais importante é a seguinte: o esquiador está metros abaixo do ponto inicial segundos depois de começar a descida.
Beleza, o primeiro passo é o seguinte: qual é a aceleração que gera uma situação como essa?
E atenção: estamos procurando o valor da aceleração paralela ao plano, ou seja, é como se estivéssemos esquecendo (por enquanto) que o plano é inclinado.
Passo 2
Se é o ponto inicial da encosta, então é o ponto onde ele se encontra quando , vamos escrever a equação do movimento do esquiador:
E como , a fórmula fica assim:
Beleza, então a gente pode afirmar o seguinte: as forças que agem sobre o esquiador estão produzindo uma aceleração (na direção paralela ao plano) de no sentido “ladeira abaixo”.
Passo 3
Quais são as forças que atuam nessa direção? O peso e a força de atrito!
Já que a normal é igual à componente do peso que é perpendicular ao plano inclinado.
Agora vamos usar a segunda lei de Newton, lembrando que o peso favorece a descida, e o atrito tenta impedi-la:
E agora podemos cortar a massa!
Resolvido!
Resposta
O coeficiente de atrito dinâmico é .