Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.2 - Ex. 51
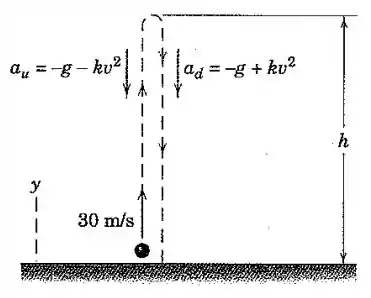
Quando o efeito de arrasto aerodinâmico é incluído, a aceleração de uma bola de beisebol movendo-se verticalmente para cima é , enquanto a aceleração quando a bola está movimento descendente é , onde é uma constante positiva e é a velocidade em metros por segundo. Se a bola é lançada para cima a aproximadamente a partir do solo, calcule a sua altura máxima e sua velocidade quando colide com o solo. Adote como e assuma que é constante.
Passo 1
Galera, vamos primeiro tentar achar a altura máxima , onde teremos velocidade nula. Como temos a expressão da aceleração em termos da velocidade, temos que usar uma equação diferencial que relacione essas três coisas: velocidade, aceleração e distância.
Então, podemos usar a seguinte equação diferencial:
Substituindo o valor de :
Passo 2
Show! Agora, vamos dar uma ajeitadinha na equação e integrá-la:
Lembre-se que a bola parte do solo com e alcança sua altura máxima com velocidade nula:
Pra calcular a integral da esquerda, lembre-se do seguinte:
Então, temos:
Se substituirmos os valores das constantes e , teremos a seguinte altura máxima:
Passo 3
Beleza! Agora vamos buscar a velocidade final . Novamente, podemos usar a equação diferencial:
Porém, a gente vai substituir o valor de , já que agora queremos analisar o movimento de descida:
Lembre-se que devemos ter velocidade nula quando a altura é máxima, e altura nula quando tivermos a velocidade final :
Passo 4
Vamos tentar isolar na equação encontrada no passo anterior:
Se substituirmos os valores das constantes e , e da altura máxima já calculada , teremos os seguintes possíveis valores de :
Como a bola foi lançada com a velocidade de e não é possível que ela retorne ao solo com um valor maior do que esse, então temos: