Enunciado
Mecânica e Resistência dos Materiais - Estatica das Estruturas por Humberto Lima Soriano- Ed: 3º - Capítulo 1.9 - Ex. 9
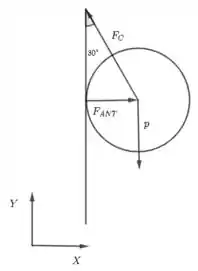
A esfera do exemplo anterior é considerada agora suspensa por um cabo e apoiada lateralmente em um anteparo vertical perfeitamente liso, como mostra a parte direita da figura anterior. Pede-se determinar o esforço nesse cabo e a força que esse anteparo exerce sobre a esfera
Passo 1
Primeiramente, vamos identificar as forças envolvidas. No sistema coordenado da figura, a força peso aponta para baixo, ou seja , (o módulo da força peso foi calculado no exercício 8) e a força que o anteparo exerce sobre a esfera aponta para a direita, ou seja , . O esforço no cabo tem componentes em e (o esforço no cabo aponta no sentido oposto a esfera):
Passo 2
Agora que identificamos as forças, vamos utilizar as equações de equilíbrio para descobrir e :
Na segunda equação, obtemos o módulo do esforço no cabo . Agora, utilizamos esse valor no resultado da primeira equação para obter o esforço no anteparo:
Passo 3
Agora que sabemos o módulo do esforço do cabo, podemos calcular suas componentes:
Resposta
,