Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.8 - Ex. 197
A esfera homogênea do Prob. 6/196 é colocada sobre a inclinação com uma velocidade angular no sentido horário, mas sem velocidade linear em seu centro (. Determine o tempo de duração do período de deslizamento. Além disso, determine a velocidade e a velocidade angular no final do período de deslizamento.
Passo 1
Este problema é semelhante ao anterior com a diferença de que o centro não possui mais velocidade linear inicial e apresenta uma velocidade angular incial . A figura abaixo representa o novo problema.
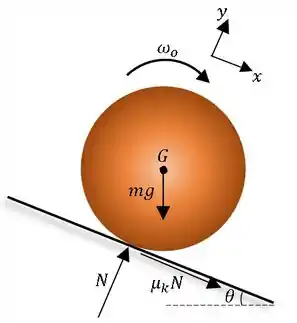
A resolução é parecida. Note que, por geometria, é possível concluir que
Sabemos que
Assim, temos
Mas sabemos também que
De onde tiramos que
Sabemos também que .
Passo 2
Simplificando, as equações obtidas são
A partir dessas equações conseguimos achar as variáveis , e em função dos parâmetros dados pelo problema. Fazendo as substituições, obtemos