Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.9 - Ex. 210

Uma barra esbelta de massa m 0 e comprimento l está soldada em seu ponto médio A na borda do disco circular macicço de massa m e de raio r . O centro do disco, que rola sem deslizar, tem uma velocidade v no instante em que A está na parte superior do disco com a barra paralela ao solo. Para esse instante, determine a quantidade de movimento angular do corpo formado, em relação a O.

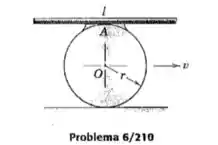
Passo 1

Pela relação entre a velocidade angular e a velocidade linear dada no enunciado:

ω = v r

Será utilizada para calcular a quantidade de movimento angular H 0 do sistema.

Passo 2

Para isso precisaremos também do momento de inercia de cada corpo individualmente. Como a rotação dos dois ocorre devido aos eixos que passam em seus centros de massa, teremos para o disco:

I D = 1 2 m d r 2

E para a barra:

I B = 1 1 2 m 0 l 2

E então fazemos as relações:

I D ω = 1 2 m d r 2 v r = 1 2 m d r v

I B ω = 1 12 m 0 l 2 v r

Passo 3

Para podermos escrever a quantidade de movimento angular:

H 0 = 1 2 m d r v + 1 12 m 0 l 2 v r + m 0 2 v r

O ultimo termo aparece devido à rotação da barra em torno do eixo do disco, ou seja a barra além de girar no próprio eixo, ela translada ao longo do arco que o ponto A faz quando o disco gira.

Resposta

H 0 = 1 2 m d r v + 1 12 m 0 l 2 v r + m 0 2 v r

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula de massa m se desloca com atrito desprezível sobre uma superfície horizontal e está conectada a uma mola leve presa em O . Na posição A a partícula tem a velocidade v A = 4m / s . Determ
A partícula de massa m é suavemente empurrada a partir da posição de equilíbrio A e posteriormente desliza ao longo da trajetória circular lisa que se situa num plano vertical. Determine o módulo da s
A partícula de massa m é lançada a partir do ponto O com uma velocidade horizontal u no instante de tempo t = 0 . Determine sua quantidade de movimento angular H O em relação ao ponto O como uma funçã
Determine o módulo H O da quantidade de movimento angular em torno do ponto de lançamento O do projétil de massa m , que é lançado com velocidade v 0 no ângulo θ conforme indicado ( a ) no instante do
A esfera de 0,2k g e seu cordão de sustentação estão girando em torno do eixo vertical sobre a superfície cônica fixa lisa com uma velocidade angular de 4r a d / s . A esfera é mantida na posição b =