Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 3.Problemas - Ex. 1
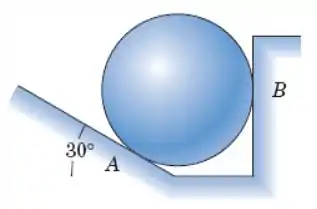
A esfera lisa e homogênea de está apoiada em uma rampa a em e apoiada contra a parede vertical lisa. Determine as forças de contato em .
Passo 1
E aí meus queridxs, tudo bom com vocês?
Se liguem só, como pela situação da questão nós temos que a esfera está em equilíbrio isso quer dizer que a resultante das forças em todas as direções deve ser igual a . Beleza, mas que forças são essas? Muito boa pergunta jovem gafanhoto
Vamos desenhar essas forças no nosso sistema
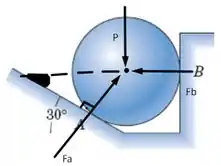
Perceba que temos um triângulo retângulo formado e pelo fato do ângulo destacado ser alterno interno com o ângulo de dado no exercício vamos ter que o ângulo que nos interessa para decompor nossa força é o de .
Passo 2
Pronto, com essa arte em mãos podemos partir pro ataque e resolver nosso problema que está, na verdade, praticamente resolvido. Para isso, vamos fazer o equilíbrio das forças em cada uma das direções a começar pela direção
De maneira análoga para o eixo teremos
Pronto, está resolvido nosso exercício sem muito problema.