Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 3.Problemas - Ex. 57
É desejável que uma pessoa seja capaz de iniciar o fechamento da porta do bagageiro de uma van, desde a posição aberta mostrada, com uma força vertical de . Como um exercício de projeto, determine a força necessária em cada um dos amortecedores hidráulicos . O centro de massa da porta de diretamente abaixo do ponto. Trate o problema como bidimensional.
Passo 1
E aí meus queridxs, tudo bom com vocês?
Vamos começar nosso problema fazendo um diagrama que explique a situação para facilitar nossa interpretação
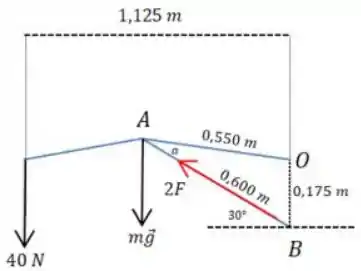
Quando a pessoa está “prestes a iniciar o fechamento da porta”, o momento total em relação ao ponto vai estar no limite do equilíbrio, então:
Pelo diagrama vemos que existem três forças contribuindo para esse momento
E para encontrar precisamos descobrir o valor de . (OBS: No desenho colocamos a força peso atuando sobre o ponto , apesar de o enunciado dizer que ela atua um pouco abaixo. Como para o momento só consideramos a distâncias perpendicular até o ponto , isso não faz diferença)
Passo 2
Vamos olhar de novo para o nosso desenho:
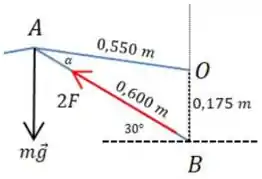
E então, pela lei dos cossenos:
Passo 3
Agora substituindo na equação do passo 1 vamos ter
Pronto, tá resolvido nosso exercício.
Resposta
A força é