Uma esfera de está sendo deslocada em um plano vertical por um braço robótico. Quando o ângulo é de , a velocidade angular do braço em torno de um eixo horizontal que passa por é de no sentido horário e sua aceleração angular é de no sentido anti-horário. Além disso, o elemento hidráulico está sendo encurtado na taxa constante de . Determine a força mínima necessária para segurar se o coeficiente de atrito estático entre a esfera e as superfícies de aperto é de . Compare com a força mínima necessária para manter a esfera em equilíbrio estático na posição de .
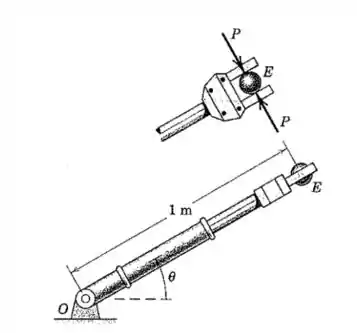
Passo 1
Sabemos que a força vai agir como a força “normal” que gera o atrito entre a esfera e as “garras” da máquina:
E multiplicamos por dois para incluir o efeito das duas garras sobre a esfera.
Ok, mas contra quem esse atrito está “lutando”? O próprio peso da bola!
Passo 2
Vamos considerar as componentes do peso nas direções radial e tangencial:
Aplicando a segunda lei de Newton em cada uma das direções, ficamos com as seguintes equações:
E o sinal negativo aparece porque essas componentes do peso estão sempre contrárias à força de atrito!
Agora podemos usar as equações em coordenadas polares para escrever essas acelerações e em termos das variáveis que foram dadas no enunciado:
E então:
Passo 3
Todos esses valores já são conhecidos (só precisamos as velocidades e acelerações de graus para radianos):
E então:
Passo 4
Então beleza, podemos somar esses dois componentes da força de atrito para encontrar o módulo da força:
Agora podemos usar a fórmula que tínhamos encontrado antes para a força de atrito para calcular a força :
Ok, agora falta comparar esse valor com a força mínima necessária para manter a esfera em equilíbrio estático na posição .
Nesse caso nem precisamos pensar nos efeitos da trajetória circular, a força total feita pela máquina precisa, pelo menos, compensar o peso da bola:
Agora sim, resolvido!
Resposta
e .