Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 77

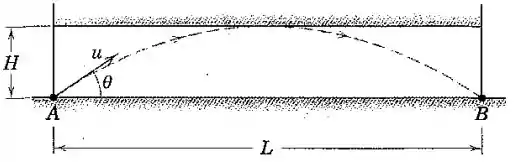
Um projétil é disparado com uma velocidade u na entrada A de um túnel horizontal de comprimento L e altura H . Determine o valor mínimo de u e o valor correspondente do ângulo θ para o qual o projétil atingirá B na outra extremidade do túnel sem tocar o topo do túnel.

Passo 1

Galera, analisando o movimento horizontal, vamos considerar que o instante t ' ocorre quando o projétil chega em B , ou seja:

x = v x t

L = u cos ⁡ θ t '

t ' = L u cos ⁡ θ

Então, na metade desse tempo, t ' / 2 , o projétil alcança sua altura máxima com velocidade nula:

v = v 0 - g t

0 = u   s e n   θ - g t ' 2

0 = u   s e n   θ - g L 2 u cos ⁡ θ

g L = 2 u 2 s e n   θ cos ⁡ θ

Passo 2

Agora, vamos calcular a altura máxima e igualar a H , para tentar achar qual seria o limite mínimo de u :

y = y 0 + v 0 t - 1 2 g t 2

H = 0 + u   s e n   θ   t ' 2 - 1 2 g t ' 2 2

H = u   s e n �� θ L 2 u cos ⁡ θ - 1 2 g L 2 4 u 2 cos 2 ⁡ θ

Vamos multiplicar tudo por 8 u 2 cos 2 ⁡ θ :

8 H u 2 cos 2 ⁡ θ = 4 L u 2 s e n θ cos ⁡ θ - g L 2

Mas lembre-se que obtivemos no passo anterior que g L = 2 u 2 s e n   θ cos ⁡ θ , apliquemos isso ao segundo termo da direita:

8 H u 2 cos 2 ⁡ θ = 4 L u 2 s e n θ cos ⁡ θ - 2 L u 2 s e n   θ cos ⁡ θ

8 H u 2 cos 2 ⁡ θ = 2 L u 2 s e n θ cos ⁡ θ

4 H cos ⁡ θ = L   s e n   θ

t g   θ = 4 H L

θ = t g - 1 4 H L

Passo 3

Vamos voltar a essa equação:

8 H u 2 cos 2 ⁡ θ = 4 L u 2 s e n θ cos ⁡ θ - g L 2

Vamos aplicar novamente g L = 2 u 2 s e n   θ cos ⁡ θ , mas agora ao primeiro termo da direita:

8 H u 2 cos 2 ⁡ θ = 2 g L 2 - g L 2

u 2 = g L 2 8 H cos 2 ⁡ θ

Então, para descobrir o valor de mínimo de u , basta saber o valor de cos ⁡ θ correspondente, mas já encontramos o valor de t g   θ :

s e n   θ cos ⁡ θ = 4 H L

1 - cos 2 ⁡ θ cos ⁡ θ = 4 H L

L 2 1 - cos 2 ⁡ θ = 16 H 2 cos 2 ⁡ θ

cos 2 ⁡ θ = L 2 L 2 + 16 H 2

Finalmente, substituímos na expressão de u :

u 2 = g L 2 8 H L 2 L 2 + 16 H 2 = g L 2 + 16 H 2 8 H = 2 g H L 2 + 16 H 2 16 H 2 = 2 g H L 2 16 H 2 + 1

u = 2 g H 1 + L 4 H 2

Resposta

u = 2 g H 1 + L 4 H 2

θ = t g - 1 4 H L

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No instante t = 10s , a velocidade de uma partícula que se desloca no plano x - y é v = 0,1i + 2jm / s . No instante t = 10,1s , sua velocidade torna-se - 0,1i + 1,8jm / s . Determine o módulo a m é d
Uma partícula que se desloca em um movimento bidimensional tem coordenadas em milímetros dadas por x = t 2 - 4 t + 20 e y = 3s e n ( 2 t ) , onde t é o tempo em segundos. Determine os módulos da veloc
Para um determinado intervalo de movimento o pino A é forçado a se deslocar na ranhura fixa parabólica pelo braço horizontal com encaixe que é elevado na direção y a uma taxa constante de 30m m / s .
Um canhão se localiza sobre uma elevação de altura h sobre o vale de um rio. Se a velocidade de disparo na boca do canhão é v0, determine a expressão para o alcance em função do ângulo de elevação da
Uma abóbora de massa 5 kg, lançada de um "canhão" feito por um aluno sob pressão atmosférica, em um ângulo de elevação de 45⁰, caiu a uma distância de 142 m do canhão. Os alunos utilizaram feixes de l