Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.7 - Ex. 179

O esguicho rotativo borrifa uma grande área circular e gira com a velocidade angular constante θ ˙ = K . Partículas de água deslocam-se ao longo do tubo em uma taxa constante l ˙ = c em relação ao tubo. Escreva expressões para os módulos da velocidade e aceleração de uma partícula de água P para uma determinada posição l no tubo rotativo.

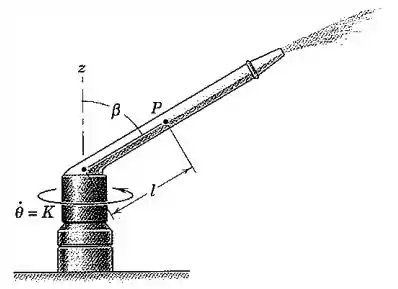
Passo 1

Considerando o eixo r como perpendicular ao eixo z , a velocidade l ˙ = c das partículas em relação ao tubo pode ser decomposta em duas componentes:

v z = l ˙ cos ⁡ β = c cos ⁡ β

v r = l ˙   s e n   β = c   s e n   β

Para o eixo θ , lembre-se:

v θ = r θ ˙

Mas θ ˙ = K e r = l   s e n   β , então:

v θ = K l   s e n   β

Tendo todas as três componentes da velocidade, podemos calcular seu módulo:

v = v r 2 + v θ 2 + v z 2 = c 2 s e n 2 β + K 2 l 2 s e n 2 β + c 2 cos 2 ⁡ β

v = c 2 + K 2 l 2 s e n 2 β

Passo 2

Agora, lembre-se de como é a aceleração em coordenadas cilíndricas:

a = r ¨ - r θ ˙ 2   e r + r θ ¨ + 2 r ˙ θ ˙   e θ + z ¨   k

Ou seja, as componentes são:

a r = r ¨ - r θ ˙ 2

a θ = r θ ¨ + 2 r ˙ θ ˙

a z = z ¨

Lembre-se de que   v r = r ˙ e v z = z ˙ , e de que v r e v z são constantes devido a velocidade em relação ao tubo ser constante. Portanto, temos r ¨ = z ¨ = 0 . E como a velocidade angular θ ˙ é constante, temos θ ¨ = 0 . Então:

a r = 0 - l   s e n   β K 2 = - K 2 l   s e n   β

a θ = 0 + 2 c   s e n   β K = 2 K c   s e n   β

a z = 0

Então o módulo da aceleração será:

a = a r 2 + a θ 2 + a z 2 = K 4 l 2 s e n 2 β + 4 K 2 c 2 s e n 2 β + 0

a = K   s e n   β K 2 l 2 + 4 c 2

Resposta

v = c 2 + K 2 l 2 s e n 2 β

a = K   s e n   β K 2 l 2 + 4 c 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em um experimento de dispersão de partículas, uma partícula alfaAé projetada com velocidadeu0= −(600 m/s)i+ (750 m/s)j− (800 m/s)kno interior de uma corrente de núcleos de átomos de oxigênio que se mo
14.25. Uma ogiva de 6 kg que se move a uma velocidade v0 (12 m/s)i (10m/s)j (400 m/s)k explode no ponto D em três fragmentos, A, B eC, que têm massa de, respectivamente, 2,5 kg, 2 kg e 1,5 kg. Sabendo
14.26. Uma ogiva de 6 kg que se move a uma velocidade v0 (12 m/s)i (10m/s)j (400 m/s)k explode no ponto D em três fragmentos, A, B eC, que têm massa de, respectivamente, 2 kg, 1,5 kg e 2,5 kg. Sabendo
14.36. Considera-se que cada um dos dois automóveis envolvidos na colisão descrita no Problema 14.35 foi projetado para resistir com segurança a um teste de impacto, em que o veículo bate em uma pared
14.42. Resolva o Problema 14.41, sabendo que a corda é partida quando 120°