Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.7 - Ex. 185
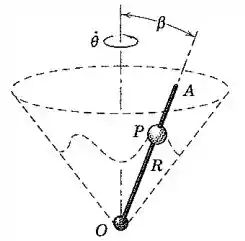
A haste é mantida no ângulo constante enquanto gira em torno do eixo vertical com uma velocidade angular constante . Simultaneamente, a esfera deslizante oscila ao longo da haste com sua distância em milímetros a partir do ponto fixo dada por , onde a frequência de oscilação ao longo da haste é constante em ciclos por segundo e onde é o tempo em segundos. Calcule o módulo da aceleração de para um instante em que sua velocidade ao longo da haste de para é um máximo.
Passo 1
Derivando a expressão de em relação ao tempo, obtemos e em função de :
Para que a velocidade seja máxima, devemos ter . Portanto, . Além disso, temos . Então:
Se pensarmos em coordenadas esféricas, os outros dados do enunciado são:
Passo 2
Agora vamos lembrar que as componentes da aceleração em coordenadas esféricas são dadas assim:
Começamos calculando :
No cálculo de , usamos a regra do produto para a derivada presente na expressão:
Passo 3
Para calcular , utilizamos novamente a regra do produto para a derivada presente na expressão:
Logo, o módulo da aceleração será: