Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 14.Problemas - Ex. 42

14.42. Resolva o Problema 14.41, sabendo que a corda é partida quando 120°

Passo 1

Vamos para mais uma questão?

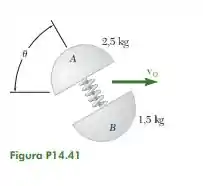
Para essa questão fica mais simples se resolvermos usando um referencial O ' que se mexe junto com a mola com velocidade v 0 . E aí, depois que calcularmos as velocidades nesse referencial, basta uma transformação de Galileu para determinar a velocidade no referencial inercial.

A gente pode começar o problema usando conservação de momento.

L i = L f

Como no primeiro instante não tem velocidade, o momento inicial é nulo, logo

0 = m A v ' A + m B v ' B

Podemos isolar v ' A

v ' A = m B m A v ' B

Passo 2

Agora usamos conservação de energia

T i = T f

O enunciado nos diz que a energia inicial é de 120   J .

120 = 1 2 m A v ' A 2 + m B v ' B 2

Mas a gente já calculou v A , então vamos substituir nessa equação

120 = 1 2 m A m B m A v ' B 2 + m B v ' B 2

Agora podemos finalmente achar uma expressão para v B

v ' B = 120 ⋅ 2 m A m B m A + m B

Vamos substituir o valor das massas

v ' B = 120 ⋅ 2 2,5 1,5 2,5 + 1,5 = 10 m s

Agora podemos calcular v A

v ' A = m B m A v ' B

Só precisamos substituir os valores

v ' A = 1,5 2,5 ⋅ 10 = 6 m s

Passo 3

Agora que temos a velocidade em O ' podemos calcular a velocidade no referencial inercial. Para isso repare que a velocidade v A faz um ângulo de 120   ° com o eixo x negativo, isso significa que faz um ângulo de 60   ° com o eixo x positivo. Então podemos calcular os vetores das velocidades como:

v A ' → = v A ' cos ⁡ 6 0 °   i ^ + sin ⁡ 6 0 °   j ^

Analogamente podemos fazer

v B ' → = v B ' - cos ⁡ 6 0 °   i ^ - sin ⁡ 6 0 °   j ^

Então os vetores são

v A ' → = 6 cos ⁡ 6 0 °   i ^ + sin ⁡ 6 0 °   j ^ = 3   i ^ + 5,2   j ^ m s

v B ' → = 10 - cos ⁡ 30 °   i ^ - sin ⁡ 30 °   j ^ = - 5   i ^ - 8,66 j ^ m s  

Passo 4

Agora basta fazer a transformação de Galileu.

v A = v A ' + v 0

v A = 3   i ^ + 5,2   j ^ + 8   i ^ = 11   i ^ + 5,2 j ^   m s  

E seu módulo fica

v A = 11 2 + 5,2 2 = 12 , 17 m s

E para calcular seu ângulo basta fazer

t g   θ = 5,2 11

θ = a r c t g 5,2 11 = 25,3 °

E

v B = v B ' + v 0 = - 5   i ^ - 8,66 j ^ + 8 i ^ = 3   i ^ - 8,66 j ^ m s

Agora vamos calcular o módulo

v B = 3 + ( - 8,66 ) 2 = 9,17 m s

E seu ângulo

θ = a r c t g - 8,66 3   = - 7 0,9 °

Resposta

a : v A = 12,17 m s   ; θ = 25,3   ° b : v B = 9,17   m s ; θ = - 70,9   °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O elemento giratório em uma câmara de mistura recebe um movimento axial periódico z = z 0s e n 2 π n t enquanto está girando na velocidade angular constante θ ˙ = ω . Determine a expressão para o módu
A partícula P se desloca ao longo da curva no espaço e tem uma velocidade v = 4 i - 2 j - km / s para o instante de tempo mostrado. No mesmo instante a partícula tem uma aceleração a cujo módulo é de
As coordenadas retangulares de uma partícula são dadas em milímetros como funções do tempo t em segundos por x = 30 cos ⁡ ( 2 t ) , y = 40s e n ( 2 t ) e z = 20 t + 3 t 2 . Determine o ângulo θ 1 entr
Um robô industrial está sendo utilizado para posicionar uma pequena peça P . Calcule o módulo da aceleração a de P para o instante em que β = 30 ° se β ˙ = 10 graus por segundo e β ¨ = 20 graus por se
O carro A está subindo uma rampa de estacionamento na forma de uma hélice cilíndrica de raio 7,2m progredindo 3m para cada meia volta. Na posição mostrada o carro tem uma velocidade de 25k m / h , que