Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas de Revisão - Ex. 155

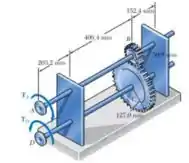
As especificações de projeto para o sistema de engrenagem e eixo de transmissão mostrados requerem que o mesmo diâmetro seja utilizado para os dois eixos e que o ângulo de torção da polia A quando submetida a um torque de 226   N * m ao mesmo tempo em que a polia D é mantida fixa não pode sofrer giro superior a 7,5°. Determine o diâmetro necessário para ambos os eixos feitos de aço com G = 77,2   G P a e tensão de cisalhamento admissível T a d m = 82,7   M P a .

Passo 1

E ai gurizada tudo belezinha? Pede para que a gente determine o diâmetro necessário para ambos os eixos feitos de aço com G = 77,2   G P a e tensão de cisalhamento admissível T a d m = 82,7   M P a . Então considere um esboço da engrenagem abaixo ;)

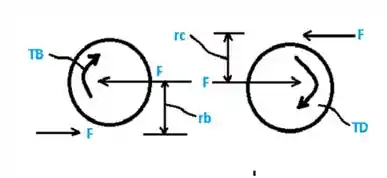
Na engrenagem B vamos fazer o somatório dos momentos.

+ ∑ M B = 0 : r B F - T A = 0       F = T B r B + ∑ M C = 0 : r C F - T D = 0 T D = r C F = r C r B T A = n T B n = r C r B = 5 2 = 2,5

Torque em eixos. T A B = T A = T B           T C D = T C = n T C = n T A

Deformações: φ C / D = T C D L G J = n T A L G J φ A / B = T A B L G J = T A L G J

Cinemática: φ D = 0           φ C = φ D + φ C D = 0 + n T A L G J r B φ B = - r C φ B             φ B = r C r B φ C = - n φ C           φ B n ² T A L G J φ A = φ C + φ B / C = n ² T A L G J + T A L G J = ( n ² + 1 ) T A L G J

Passo 2

Diâmetro com base na tensão.

Maior torque: T m = T C D = n T A T m = T m c J = 2 n T A π c ³ =           τ m =     τ a l l = 82,7   M P a ,     T A = 2 226   N m c = 2 n T A π τ m 3 = 0,032639   m

Diâmetro com base no limite de rotação. φ = 7,5 ° = 0,1309   r a d φ = n 2 + 1 T A L G J = 2   x   7,25   x   T A L π c 4 G       L = 0,6096   m . c = 2   x   7,25   x   T A L π G φ 4 = 0,0316738   m

Escolha o diâmetro maior.

Resposta

d = 0,032639   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O dispositivo serve como uma mola de torção compacta. É feito de aço A-36 e composto por um eixo interno maciço C B embutido em um tubo A B e acoplado a esse tubo por um anel rígido em B . Podemos con
O eixo de aço A-36 tem diâmetro de 50m m e está preso nas extremidades A e B . Se for submetido ao momento, determine a tensão de cisalhamento máxima nas regiões A C e C B do eixo.
O tubo de bronze C 86100 tem diâmetro externo de 37,5m m e espessura de 0,3m m . A conexão C está sendo apertada com uma chave de torque. Se o torque desenvolvido em A for 16N . m , determine o valorF
O contorno da superfície do eixo é definido pela equação y = e a x , onde a é uma constante. Se o eixo for submetido a um torque T em suas extremidades, determine o ângulo de torção na extremidade A e
Uma mola cilíndrica é composta por um anel de borracha preso a um anel e eixo rígidos. Se o anel for mantido fixo e um torque T for aplicado ao eixo rígido, determine o ângulo de torção do eixo. O mód