Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 6.Problemas - Ex. 49
6/46) Uma mulher pedala sua bicicleta à velocidade constante em uma estrada escorregadia com inclinação de . A mulher e a bicicleta têm uma massa combinada de , com centro de massa em . Se a roda traseira está na iminência de escorregar , determine o coeficiente de atrito entre o pneu traseiro e a estrada . Se o coeficiente de atrito fosse duplicado , qual seria a força de atrito atuando sobre a roda traseira? (Por que podemos desprezar o atrito sob a roda dianteira? )
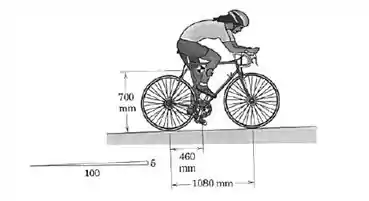
Passo 1
Então galera , a primeira coisa que devemos fazer é calcular o ângulo de inclinação da estrada . Neste caso , temos que :
Com isso podemos calcular a componente vertical e horizontal da reação a força peso do sistema , respectivamente , através das relações :
Passo 2
Bom pessoal , seja o ponto de contato da roda dianteira com a estrada , podemos aplicar a equação de equilíbrio do momento em relação ao ponto pela fórmula :
:
Logo ,
E aplicando a equação de equilíbrio do sistema em relação ao eixo , obtemos que :
Passo 3
Agora precisaremos lembrar da relação :
Sendo assim ,
Substituindo os valores encontrado no passo anterior , achamos que :
Cabe ressaltar que se o fosse dobrado , a força de atrito permaceneria . Isso se deve porque , analisando o equilíbrio no eixo , temos que :
Logo ,
Sendo assim , mostramos que o valor da força de atrito nesse caso não depende do coeficiente de atrito da estrada .
Resposta
Se o fosse dobrado , a força de atrito permaceneria .
Tranquilo pessoal? Então partiu resolver mais questões