Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.7 - Ex. 76
Em uma estação de carregamento a granel, o cascalho sai do funil alimentador na taxa de com uma velocidade de na direção mostrada e é depositado sobre o caminhão plataforma em movimento. A força de tração entre as rodas motrizes e a estrada é , que supera os da resistência por atrito da estrada. Determine a aceleração do caminhão segundos após o funil alimentador ser aberto sobre a plataforma do caminhão, instante no qual o caminhão possui uma velocidade para frente de . A massa do caminhão vazio é .
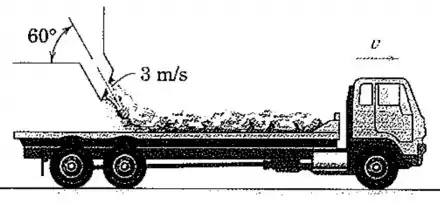
Passo 1
Vamos analisar a soma das forças externas que agem sobre o caminhão na direção horizontal:
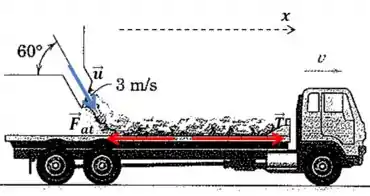
E sabemos que essa soma das forças externas em precisa ser igual à derivada do momento linear nessa mesma direção:
Passo 2
O cascalho sai do funil a uma taxa de , e faz com que a massa do caminhão aumente com o tempo, então:
Como a velocidade do caminhão é de para frente, ou , a velocidade do cascalho em relação ao caminhão, na direção horizontal, é:
E qual é a massa do caminhão? Bom, ela varia com o tempo, mas o enunciado pediu para calcularmos tudo segundos após a abertura do funil, ou seja:
Passo 3
Agora vamos substituir tudo na nossa fórmula anterior:
E essa é a aceleração do caminhão para frente:
Resposta
A aceleração é .