Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 8

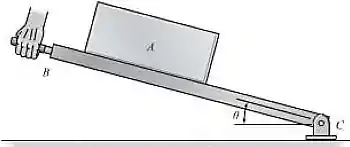
Se o bloco A de 5 kg escorrega para baixo no plano inclinado com uma velocidade constante quando θ = 30 0 ,   determine a aceleração do bloco quando θ   =   45 0 .

Passo 1

Inicialmente, o bloco de 5 kg escorrega no plano inclinado a 30 0 com velocidade constante. Isso quer dizer que o bloco não possui aceleração, visto que sua velocidade não varia. A   45 0 , o bloco escorrega e sua velocidade deixa de ser constante. Para determinar a aceleração do corpo quando θ = 45 0 , devemos, inicialmente, obter a equação do movimento quando θ = 30 0 . Do diagrama de corpo livre, temos:

∑ F y ' = m a y '

N - P cos ⁡ 30 = m a y '

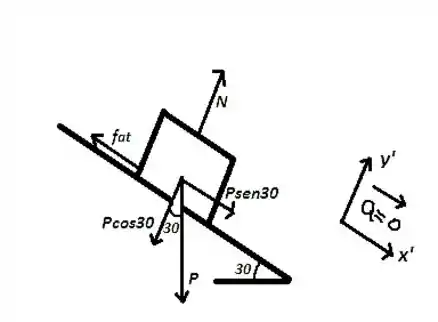
Como não há movimento na direção y ' , podemos chegar a seguinte conclusão:

N - P cos ⁡ 30 = m × 0

N = P cos ⁡ 30

Por definição:

P = m g

f a t = μ N

Assim:

N = m g cos ⁡ 30 = ( 5 × 9,81 ) cos ⁡ 30

N = 42,478 N

∑ F x ' = m a x '

P sin ⁡ 30 - f a t = m a x '

m g sin ⁡ 30 - μ N = m × 0

m g sin ⁡ 30 - μ N = 0

Na equação acima, podemos encontrar o coeficiente de atrito μ entre a caixa e o plano que terá um valor igual tanto para θ = 30 0 quanto para θ = 45 0 :

μ = m g sin ⁡ 30 N = ( 5 × 9,81 ) sin ⁡ 30 42,478 = 0,5773

Passo 2

O próximo passo e obter a equação do movimento, agora, com θ = 45 0 e determinar a aceleração do bloco. Do diagrama de corpo livre, temos:

∑ F y ' = m a y '

N ' - P cos ⁡ 45 = m a y '

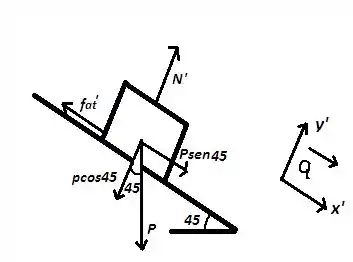
Como não há movimento na direção y ' , chegaremos a seguinte conclusão:

N ' - P cos ⁡ 45 = m × 0

N ' = P cos ⁡ 45

N ' = m g cos ⁡ 45 = ( 5 × 9,81 ) cos ⁡ 45

N ' = 34,684 N

∑ F x ' = m a x '

P sin ⁡ 45 - f a t ' = m a x '

m g sin ⁡ 45 - μ N ' = m a x '

Isolando a aceleração a x ' na equação acima, temos:

a x ' = m g sin ⁡ 45 - μ N ' m

Passo 3

Substituindo os valores da massa m do bloco, coeficiente de atrito μ e a normal N ' , na equação acima, podemos encontrar o seguinte valor para aceleração do bloco:

a x ' = ( 5 × 9,81 ) sin ⁡ 45 - ( 0,5773 × 34,684 ) 5

a x ' = 2,932   m / s 2

Resposta

A aceleração do bloco quando θ   =   45 0 é igual a 2,932   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A massa m de uma gota de chuva aumenta conforme ela assimila umidade durante a sua descida vertical através do ar parado. Se a resistência do ar ao movimento da gota é R e sua velocidade para baixo é
A haste do magnetômetro de uma nave espacial é constituída por um grande número de unidades com formato triangular que emergem para sua configuração de operação após a liberação a partir do recipiente
No instante do lançamento vertical o foguete expele os gases de exaustão na taxa de 220k g / s com uma velocidade de exaustão de 820m / s . Se a aceleração vertical inicial é 6,80m / s 2 , calcule a m
Um rolo de cabo flexível pesado com um comprimento total de 100 metros e uma massa de 1,2k g / m deve ser estendido ao longo de uma linha reta horizontal. A extremidade está presa a uma estaca em A ,
Quando o foguete atinge a posição mostrada em sua trajetória, ele possui uma massa de 3 t e está além do efeito da atmosfera terrestre. A aceleração gravitacional é 9,60m / s 2 . O combustível está se