Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.5 - Ex. 81
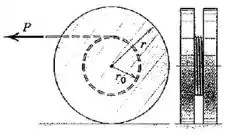
Qual deve ser o raio do encaixe circular para que não haja força de atrito agindo entre o carretel e a superfície horizontal independentemente do módulo da força aplicada ao cabo? O raio de giração centroidal do carretel é .
Passo 1
Vamos começar escrevendo o momento de inércia em relação ao ponto em que o carretel está em contato com a superfície.
Precisamos do teorema dos eixos paralelos:
E nesse caso o momento de inércia em relação ao centro de massa pode ser escrito em função do raio de giração :
E a distância entre o centro de massa e o ponto é o raio do carretel, então:
E então se calcularmos o momento total em relação ao ponto vamos ficar com a seguinte expressão:
E a única força que produz momento em torno do ponto é a força , que está a uma distância do ponto :
Passo 2
Até aqui temos uma equação com duas variáveis desconhecidas: e . Vamos escrever mais uma equação para poder resolver o problema, dessa vez utilizando a segunda lei de Newton na direção horizontal:
E a única força que age nessa direção é , e a aceleração é dada por :
Então nosso sistema é:
Vamos multiplicar a equação de cima por e então dividir a primeira pela segunda:
E isolando :
Resposta
O raio do encaixe circular deve ser .