Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 70

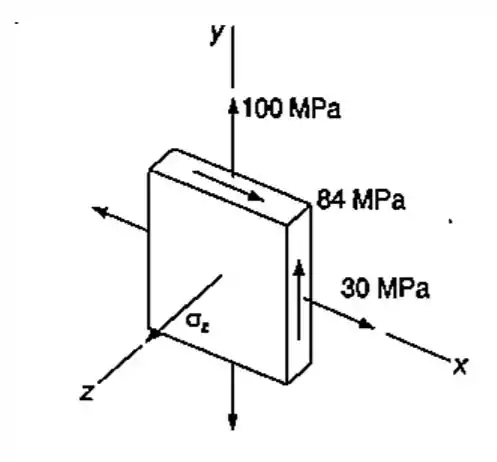
Para o estado plano de tensões mostrado, determinar a máxima tensão de cisalhamento, quando: (a) σ z = 0   M P a ; (b) σ z = + 60   M P a ; (c) σ z = - 60   M P a .

Passo 1

Para resolver essa questão a primeira coisa e a mais importante é saber identificar corretamente as tensões normais e cisalhantes, neste caso será o seguinte:

σ x = 3 0   M P a

σ y = 10 0   M P a

τ x y = 84   M P a

Depois vamos calcular a tensão normal média e o raio do ciclo de mohr. Com isso vamos poder achar a tensão cisalhante máxima.

Passo 2

Vamos achar a tensão média, que é o centro do ciclo de mohr da seguinte forma:

σ m é d = σ x + σ y 2

σ m é d = 3 0 + 100 2

σ m é d = 65   M P a

Passo 3

Achar o raio do ciclo de Mohr:

R = σ x - σ y 2 2 + τ y z 2

R = 30 - ( 100 ) 2 2 + 84 ²

R = 8281

R = 91   M P a

Passo 4

Para achar a tensão cisalhante nos pontos extremos co círculo (A e B):

σ A = σ m é d + R

σ A = 65 + 91 = 156   M P a

σ B = σ m é d - R

σ B = 65 - 91 = - 26   M P a

Passo 5

Para a letra A vamos ter:

σ z = 0

τ m á x = 1 2 σ m á x - σ m í n

τ m á x = 1 2 156 - ( - 26 )

τ m á x = 91   M P a

Passo 6

Para a letra B vamos ter:

σ z = + 60   M P a

τ m á x = 1 2 σ m á x - σ m í n

τ m á x = 1 2 156 - ( - 26 )

τ m á x = 91   M P a

Passo 7

Para a letra C vamos ter:

σ z = - 60   M P a

τ m á x = 1 2 σ m á x - σ m í n

τ m á x = 1 2 156 - ( - 6 0 )

τ m á x = 108   M P a

Resposta

a)

τ m á x = 91   M P a

b)

τ m á x = 91   M P a

c)

τ m á x = 108   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

80. O círculo de Mohr para o estado de tensão na Figura 9.15a é mostrado na Figura 9.15b. Mostre que determinar as coordenadas do ponto P ( σ x ' , τ x ' y ' ) no círculo dá o mesmo valor que as equaç
76. Determine(a) as tensões principais e (b) a tensão de cisalhamento máxima no plano e a tensão normal média. Especifique a orientação do elemento em cada caso.
A barra retangular em balanço está sujeita à força de 25 kN. Determine as tensões principais no ponto B.
A manivela do pedal de uma bicicleta tem a seção transversal mostrada na figura. Se ela estiver presa à engrenagem em B e não girar quando submetida a uma força de 400 N, determine as tensões principa
A estrutura suporta a carga distribuída de 200 N/m. Determine a tensão normal e a tensão de cisalhamento no ponto E que agem nos sentidos perpendicular e paralelo às fibras, respectivamente. Nesse pon