Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 55
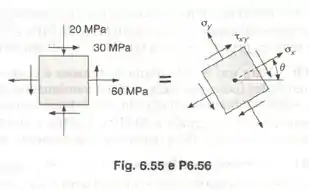
Para o estado plano de tensões mostrado, determinar a variação dos valores de , para que a intensidade de tensão de cisalhamento seja igual ou inferior que .
Passo 1
O que a gente precisa fazer aqui é usar o Círculo de Mohr para descobrir os intervalos para nos quais o cisalhamento após a rotação tenha a intensidade máxima de .
E como a gente faz isso? Vamos tentar montar esse círculo com as informações que a gente tem. Vamos listar:
- a tensão normal no eixo é positiva porque está saindo da seção e vale:
- a tensão normal no eixo é negativa porque está entrando na seção e vale:
- tensão de cisalhamento está no sentido positivo e vale:
Bora começar!
Passo 2
Achando a coisinhas que a gente precisa para montar o Círculo de Mohr, vamos achar as coordenadas de , e o centro . Temos que:
Colocando essas coisas no Círculo:
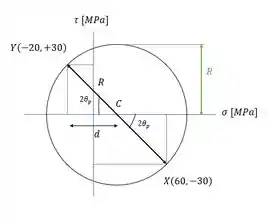
Passo 3
Aí a gente consegue achar o raio com as relaçõezinhas de triângulo retângulo:
E :
Passo 4
Tá, e agora o que a gente faz com isso tudo? Bem a gente marca no Círculo onde :
Conseguimos tirar essa relação daí:
Repara que para chegar em , ele precisa girar no sentido horário, um ângulo que vale:
Já para chegar em , vai precisar girar no sentido anti-horário, um ângulo que vale:
Aí nosso primeiro intervalinho fica:
A gente pode fazer o mesmo raciocínio para chegar em e pelo sentido anti-horário:
Aí nosso segundo intervalo fica:
Resposta
e