Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 131

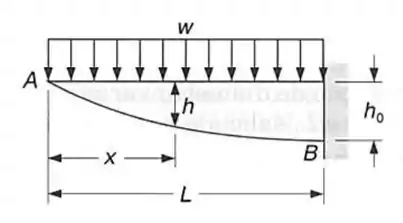
A viga AB tem uma seção transversal retangular de largura b constante e altura h variável. Sabendo que a viga deve ser de resistência constante, expressar h em termos de x, L e ho.

Passo 1

Fala aíi gurizada tudo belezinha, espero que simm!!!! Para entendermos melhor a questão vamos fazer um esquema de diagrama de corpo livre? Vejam abaixo!!!

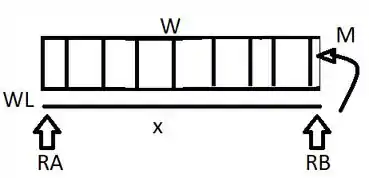
Gurizada primeiramente vamos realizar o somatório em Y para encontrarmos as reações RA e RB, vem comigo !!!

+ ↑ ∑ F y = 0

R A + R B - W L = 0

Vamos considerar o estado de equilíbrio e que as reações são iguais, então temos:

R A = R B = W L

Agora partiu fazer o momento em B? vem comigoo!!!

+ ↶ ∑ M b = 0

W L × x - w x × x 2 + M = 0

M = w x × ( L + x 2 )

Encontrando a seção temos a seguinte equação:

S = M σ = w x × ( L + x 2 ) σ

Passo 2

Galera considerando a seção retangular da viga temos que :

S =

Então podemos substituir na equacao acima ;)

b h 2 6 = w x × ( L + x 2 ) σ

Agora temos que isolar o “h” :D

h = 6 × ( w x × L + x 2 ) b × σ

Considerando que X= L (comprimento da viga temos que substituir na equação

h = 6 × ( w x × x + x 2 ) b × σ = 6 w × 9 x ² b × σ

Vamos considerar que h=h0= 6 w × 9 x ² b × σ

Resposta

h = h o 6 w × 9 x ² b × σ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas placas de aço são mantidas juntas através de parafusos de aço de alta resistência com 16 mm de diâmetro perfeitamente ajustados no interior de espaçadores cilíndricos de latão. Sabendo que a tens
Na estrutura de aço mostrada na figura é utilizado um pino de 6 mm de diâmetro em C e são utilizados pinos de 10 mm de diâmetro em B e D. O limite da tensão de cisalhamento é 150 MPa em todas as conex
As duas partes do elemento AB são coladas ao longo de um plano formando um ângulo θ com a horizontal. Sabendo que o limite de tensão para a junta colada é 17,24 MPa em tração e 8,96 MPa em cisalhament
Uma força P é aplicada a uma barra de aço encaixada dentro de um bloco de concreto, conforme mostra a figura. Determine o menor comprimento L para o qual pode ser desenvolvida a tensão normal admissív
As duas partes do elemento AB são coladas ao longo de um plano formando um ângulo θ com a horizontal. Sabendo que o limite de tensão para a junta colada é de 17,2 MPa em tração e de 9 MPa em cisalhame