Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 10.Problemas - Ex. 95
O estado de tensão que age em um ponto crítico sobre uma chave de porca é mostrado na figura. Determine a menor tensão de escoamento para o aço que poderia ser selecionado para a fabricação da ferramenta com base na teoria de cisalhamento máxima.
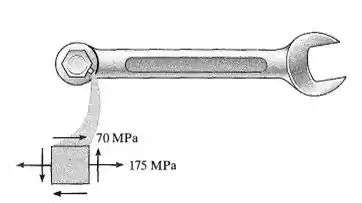
Passo 1
Fala, querido! Bora lá!
Para achar a tensão de escoamento a partir dessa teoria que ele pede, precisamos achar as tensões principais nesse estado plano de tensões.
E para achar essas tensões principais, a gente precisa entender que tensões temos ali no elemento com o sinal certinho:
Primeiramente, dizemos que:
Porque a setinha está saindo da seção normal a direção horizontal. E dizemos que
Porque não tem setinha saindo da seção normal a direção vertical. E por fim:
Porque as setas apontam para o primeiro e terceiro quadrante.
Vamos seguir!
Passo 2
Usamos essa fórmulinha para chegar nas tensões principais:
Para :
E para :
Passo 3
Segundo a teoria da tensão de cisalhamento máxima, como as tensões possuem sinais diferentes, devemos determinar a tensão mínima de escoamento aceitável pela fórmula:
Logo: