Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 52

A viga está sujeita ao carregamento mostrado na figura, onde P = 7 k N . Determine a tensão de cisalhamento média desenvolvida nos pregos no interior da região AB da viga. Os pregos estão localizados em cada lado da viga e espaçados de 100   m m

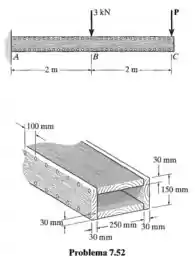
Passo 1

Dados da questão: P = 7 k N ,   s = 100 m m ,   d = 5 m m

A questão pede a tesão cisalhante sobre o prego: τ p r e g o = ?

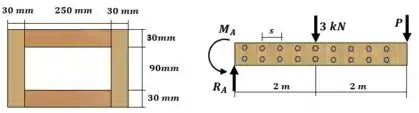
Estratégia de resolução: Vamos começar calculando as reações de apoio no ponto A. Observe que o ponto A será o ponto de maior esforço cortante interno.

Depois poderemos definir o momento de inércia da seção transversal. Não é preciso calcular o centroide, pois a seção transversal é perfeitamente simétrica, e por isso seu centroide é no seu centro.

Após isso podemos usar a equação de fluxo de cisalhamento para definir a forçar que atua em um prego. E com essa força podemos calcular o cisalhamento que atua em um prego.

Passo 2

Calculando as reações de apoio:

∑ F y = 0 ⇒ R A - 3 - P = 0

R A = 3 + P

R A = 10 k N

∑ M A = 0 ⇒ M A - 3 ⋅ 2 - P ⋅ 4 = 0

M A = 6 + 4 P

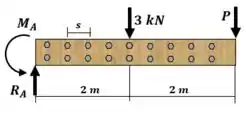
Como o ponto A é o ponto de maior esforço interno, então: V = 10   k N

Passo 3

Agora podemos calcular o momento de inércia. Podemos simplesmente calcular o momento de inércia de um retângulo sólido e subtrair o momento de inércia correspondente ao retângulo vazio

I = 310 ⋅ 150 3 12 - 250 ⋅ 90 3 12 = 72 ⋅ 10 6 m m 4

I = 72 ⋅ 10 - 6 m 4

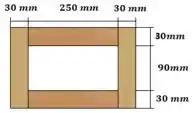
Passo 4

Mas antes de podermos aplicar a equação de fluxo de cisalhamento, precisamos calcular o momento estático na região dos pregos. A região escolhida esta destacada:

Q = 250 ⋅ 30 ⋅ 60 = 450000 m m 3

Q = 45 ⋅ 10 - 5 m 3

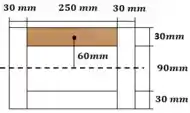
Passo 5

Perceba que a seção que selecionamos está em contato com duas chapas laterais, e gerando um cisalhamento sobre dois pregos. A relação entre o prego e fluxo de cisalhamento é:

q = 2 F p r e g o s

O número dois aparece na equação acima, há dois pregos sobre o mesmo fluxo de cisalhamento.

Por outro lado, a fórmula para o fluxo de cisalhamento é

q = V ⋅ Q I

Igualando as duas equações:

V ⋅ Q I = 2 F p r e g o s

Isolando V

F p r e g o = V Q s 2 I

Substituindo os valores:

F p r e g o = 10 k N ⋅ 45 ⋅ 10 - 5 m 3 ⋅ 0,1   m 2 ⋅ 72 ⋅ 10 - 6 m 4

F p a r a f u s o = 3,125   k N

Passo 6

Por fim, basta calcular a tensão cisalhante sobre o prego.

A área de seção transversal do prego é:

A = d 2 π 4

A = 25 π 4   m m 2

Então a tensão de cisalhamento no prego é:

τ p r e g o = F A

τ p r e g o = 3,125 25 π 4 ⋅ k N m m 2

τ p r e g o = 159   M P a

Resposta

τ p r e g o = 159   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Trace os diagramas de força cortante e momento fletor para a viga W310x21 e verifique se ela suportará com segurança a carga mostrada na figura. A tensão de flexão admissível é σ a d m = 160M P a e a
A viga simplesmente apoiada é composta por duas seções W310x33 montadas como mostra a figura. Determine a carga uniforme máxima w que ela suportará se a tensão de flexão admissível for σ a d m = 160M
Selecione no apêndice B a viga de aço de abas largas de menor peso que suportará com segurança as cargas mostradas na figura. A tensão de flexão admissível é σ a d m = 160M P a e atenção de cisalhamen
A viga será usada para suportar uma máquina que tem peso de 80k N e centro de gravidade em G. Se a tensão de flexão máxima não puder ultrapassar σ a d m = 160M P a , determine a largura b exigida para
A viga composta foi feita com duas seções unidas por um pino em B. Use o Apêndice B e selecione a viga de abas largas leve que seria segura para cada seção, se a tensão de flexão admissível for σ a d