Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 10.Problemas - Ex. 82
O estado de tensão que age sobre um ponto crítico em um elemento de máquina é mostrado na figura. Determine a menor tensão de escoamento para um aço que possa ser selecionado para a fabricação da peça com base na teoria da tensão de cisalhamento máxima.
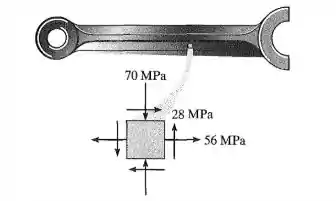
Passo 1
Primeiramente, sabemos que:
Logo, as tensões principais serão dadas por:
Substituindo os dados e fazendo a conta, teremos:
Passo 2
Agora, como as tensões possuem sinais diferentes, devemos determinar a tensão máxima pela fórmula:
Logo:
Resposta
Exercícios de Livros Relacionados
Uma liga de alumínio deve ser usada para fabricar um eixo de acionamento maciço que transmite25k W a 1.200 rev/min. Usando um fator de segurança de 2,5 para escoamento, determine o menor diâmetro do e
As tensões principais que agem em um ponto sobre um vaso de pressão cilíndrico de parede fina são σ 1=p r / t , σ 2=p r / 2 teσ 3=0 . Se a tensão de escoamento for σ y , determine o valor máximo de p
As tensões principais no plano que agem sobre um elemento diferencial são mostradas na figura. Se o material for aço-máquina com tensão de escoamento σ y = 700 MPa, determine o fator de segurança para
Resolva o Problema 10.83 usando a teoria da tensão de cisalhamento máxima.
Se uma peça máquina for feita de titânio (Ti-6A1-4v) e um ponto crítico no material tiver as tensões principais σ 1 e σ 2 = σ 1 0,5 , determine o valor de σ 1 que provocará escoamento de acordo com (a