Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 10.Problemas - Ex. 81
As tensões principais no plano que agem sobre um elemento diferencial são mostradas na figura. Se o material for aço-máquina com tensão de escoamento = 700 MPa, determine o fator de segurança para escoamento, se for considerada a teoria da tensão de cisalhamento máxima.
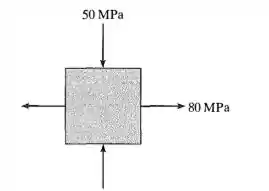
Passo 1
Primeiramente, sabemos que:
Como não temos tensão cisalhante, essas já são as tensões principais.
Logo,como as tensões tem sinais contrários, devemos usar a expressão:
Substituindo, teremos:
Resposta
Exercícios de Livros Relacionados
O estado de tensão que age em um ponto crítico sobre uma chave de porca é mostrado na figura. Determine a menor tensão de escoamento para o aço que poderia ser selecionado para a fabricação da ferrame
Se um eixo maciço de diâmetro d for submetido a um torque T e um momento M, mostre que, pela teoria da σ a d m = 16 π d 3 M + M 2 + T 2 .
O estado de tensão que age sobre um ponto crítico na estrutura de um banco de automóvel durante uma colisão é mostrada na figura. Determine a menor tensão de escoamento para um aço que possa ser selec
Uma liga de alumínio deve ser usada para fabricar um eixo de acionamento maciço que transmite25k W a 1.200 rev/min. Usando um fator de segurança de 2,5 para escoamento, determine o menor diâmetro do e
As tensões principais que agem em um ponto sobre um vaso de pressão cilíndrico de parede fina são σ 1=p r / t , σ 2=p r / 2 teσ 3=0 . Se a tensão de escoamento for σ y , determine o valor máximo de p