Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 63
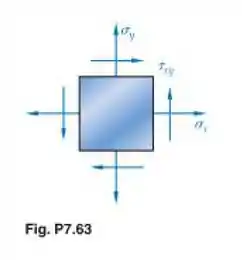
Para o estado de tensão mostrado, sabe-se que as tensões normal e de cisalhamento estão direcionadas conforme mostra a figura e que = 96,5 MPa, = 62,1 MPa e = 34,5 MPa. Determine (a) a orientação dos planos principais, (b) a tensão principal e (c) a tensão de cisalhamento máxima no plano das tensões.
Passo 1
Opaa! Fala pessoal, beleza? Bora pra mais um?! Para resolver esse exercício, vamos ter que desenhar o círculo de Mohr para o estado de tensões dado. Só que para desenhar o círculo, precisamos de algumas informações. Vamos precisar da tensão média, do raio do círculo de Mohr e da tensão de cisalhamento para o estado de tensão, que não foi dada.
Depois disso, com o círculo desenhado, conseguimos encontrar a orientação dos planos principais pedida na letra (a). Depois para a letra (b), conseguimos encontrar a tensão máxima no plano das tensões através da tensão média e do raio do círculo.
E, para a letra (c), basta a gente lembrar que a tensão de cisalhamento máxima no plano das tensões é o próprio raio do círculo!
Passo 2
Vamos começar escrevendo nossas componentes de tensão que vem do elemento dado no enunciado, onde temos:
Agora, vamos calcular a tensão média, que é dada por:
Agora, sabemos que o raio do círculo de Mohr pode ser encontrado através da seguinte relação:
Então, substituindo os valores conhecidos nessa equação, temos:
Agora, temos uma outra equação para o raio do círculo de Mohr, que é dada por:
Então, isolando a tensão de cisalhamento, teremos:
Substituindo os valores conhecidos, chegamos em:
Agora, como o enunciado nos disse que as tensões no elemento dado já estavam na orientação correta, de acordo com a imagem, a nossa tensão de cisalhamento será positiva, então teremos:
Passo 3
Beleza! Com esses dados conseguimos esboçar nosso círculo de Mohr, que será dado por:
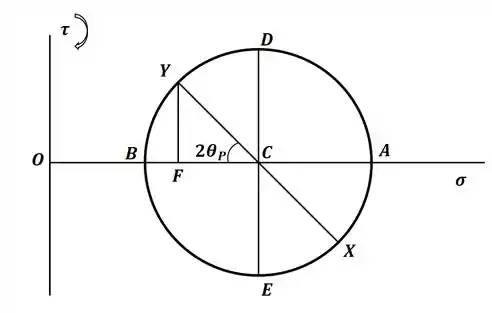
Beleza! Então, com o círculo de Mohr, podemos encontrar as direções principais por trigonometria, onde teremos:
Substituindo os valores conhecidos, chegamos em:
Beleza, essa é uma das direções principais, sabemos que a outra fica a 180° do círculo de Mohr, ou seja, a 90° de rotação do elemento diferencial, então teremos:
Fechamos a letra (a). Bora pra (b), agora vai ser rápido, prometo!
Passo 4
Beleza! Para a letra (b), nós sabemos que a tensão principal é dada por:
Então, substituindo os valores conhecidos, chegamos em:
Pra finalizar, bora pra (c).
Passo 5
Agora, para a letra (c), conforme vimos no passo 1, basta a gente lembrar que a tensão de cisalhamento máxima no plano das tensões é o próprio raio do círculo, então temos:
Feshooow!