Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 104
O estado de tensão num ponto um membro é mostrada no elemento. Determinar os componentes de tensão que actuam sobre o plano inclinado AB.
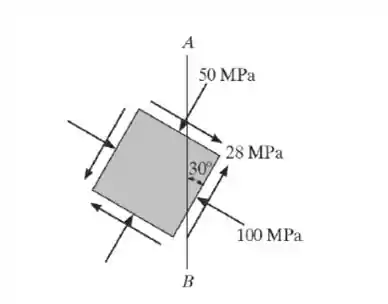
Passo 1
Fala aí galera, este problema é bem simples. Primeiramente, vamos calcular a tensão média atuante que será o centro do círculo de Mohr:
Agora, vamos calcular o raio do círculo de Mohr para que possamos achar as tensões principais:
Passo 2
Com os dados calculados e o ângulo dado, podemos achar as tensões pedidas da seguinte forma:
Resposta
Exercícios de Livros Relacionados
5. O estado de tensão em um ponto em um elemento estrutural é mostrado no elemento. Determine as componentes de tensão que agem no plano inclinado A B . Resolva o problema usando o método do equilíbri
Determine o estado de tensão equivalente, se um elemento estiver orientado a 40º em sentido horário em relação ao elemento mostrado. Use o círculo de Mohr.
O vaso de pressão cilíndrico tem raio interno de 1,25m e espessura de parede de 15m m . É feito de chapas de aço soldadas ao longo de uma linha de junção a 45 ° em relação à horizontal. Determine as c
Determine o estado de tensão equivalente em um elemento se ele estiver orientado a 30º em sentido horário em relação ao elemento mostrado. Use as equações de transformação de tensão.