Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 100
Determine o estado de tensão equivalente, se um elemento estiver orientado a 40º em sentido horário em relação ao elemento mostrado. Use o círculo de Mohr.
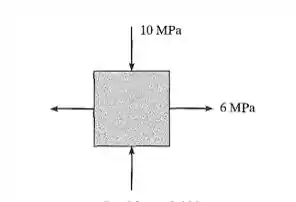
Passo 1
Fala aí galera, vamos para a resolução de mais um problema. Primeiramente, vamos calcular as tensões médias atuantes que serão o centro do círculo de Mohr:
O próximo passo será calcular o raio do círculo para que possamos determinar as tensões principais:
Passo 2
Utilizando os dados obtidos e o ângulo dado, podemos calcular as tensões pedidas. Estas serão dadas por:
Resposta
Exercícios de Livros Relacionados
25. Um bloco de madeira falhará, se a tensão de cisalhamento que age ao longo da fibra for 3,85M P a . Se a tensão normal σ x = 2,8M P a , determine a tensão de compressão σ y necessária para provocar
2. O estado de tensão em um ponto em um elemento estrutural é mostrado no elemento. Determine as componentes de tensão que agem no plano inclinado A B . Resolva o problema usando o método do equilíbri
O estado de tensão em um ponto em um elemento estrutural é mostrado no elemento. Determine as componentes de tensão que agem no plano inclinado A B . Resolva o problema usando o método do equilíbrio d
3. O estado de tensão em um ponto em um elemento estrutural é mostrado no elemento. Determine as componentes de tensão que agem no plano inclinado A B . Resolva o problema usando o método do equilíbri
6. O estado de tensão em um ponto em um elemento estrutural é mostrado no elemento. Determine as componentes de tensão que agem no plano inclinado A B . Resolva o problema usando o método do equilíbri