Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 33
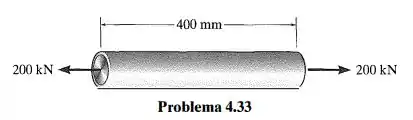
O tubo de aço A-36 tem núcleo de alumínio e está sujeito a uma força de tração de . Determine a tensão normal média no alumínio e no aço devido a essa carga. O tubo tem diâmetro externo de e diâmetro interno de .
Passo 1
Primeiro, vamos calcular a força para o concreto e para o aço:
Passo 2
Agora, temos que aplicar a fórmula para cada um:
Passo 3
Resolvendo este sistema linear, temos:
Agora, basta substituirmos:
Para o alumínio, temos:
Resposta
Exercícios de Livros Relacionados
O conjunto é composto por três hastes de titânio ( T i- 6 A 1 - 4 V ) e uma barra rígida A C . A área da seção transversal de cada haste é dada na figura. Se uma força de 30k N for aplicada ao anel F
Um suporte para tudos apoiado por molas é composto por duas molas que, na posição original, não estão alongadas e têm rigidez k=60k N / m , três hastes de aço inoxidável 304 , A BeC D , com diâmetro d
Um suporte para tubos apoiado por molas é composto por duas molas que, na posição original, não estão alongadas e têm rigidez k = 60 k N / m , três hastes de aço inoxidável 304 ,A BeC D , com diâmetro
A carga é sustentada pelos quatro cabos de aço inoxidável 304 conectados aos elementos rígidos A B e D C . Determine o deslocamento vertical da carga de2,5k N se os elementos estiverem na horizontal q
A peça fundida é feita de um material com peso espedfico γ e módulo de elasticidade E . Se ela tiver a forma da pirilmide cujas dimensões são mostradas na figura, determine até que distância sua extre