Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 14

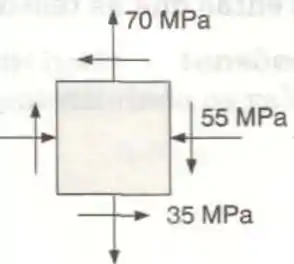
Para o estado de tensões dado, determinar as tensões, normal e de cisalhamento, depois que o elemento mostrado tenha sofrido uma rotação de: (a) 40°, no sentido anti-horário; (b) 15°, no sentido horário.

Passo 1

Para resolver essa questão a primeira coisa e a mais importante é saber identificar corretamente as tensões normais e cisalhantes, neste caso será o seguinte:

σ x = - 5 5   M P a

σ y = 7 0   M P a

τ x y = - 35   M P a

Depois disso vamos aplicar os efeitos da rotação.

Passo 2

Agora vamos descobrir as tensões máxima e mínima:

σ m á x = σ x + σ y 2

σ m á x = - 55   + 70 2

σ m á x = 7,5   M P a

Agora a tensão mínima

σ m í n = σ x - σ y 2

σ m í n = - 55   - 70 2

σ m í n = - 6 2,5   M P a

Passo 3

Aplicar as equações de rotação:

σ x ' = σ x + σ y 2 + σ x - σ y 2 ⋅ cos ⁡ 2 θ + τ x y ⋅ s e n ( 2 θ )

σ y ' = σ x + σ y 2 - σ x - σ y 2 ⋅ cos ⁡ 2 θ - τ x y ⋅ s e n ( 2 θ )

τ x y ' = - σ x - σ y 2 ⋅ sen ⁡ 2 θ + τ x y ⋅ c o s ( 2 θ )

Passo 4

Para a letra A onde a rotação é de 40° no sentido anti horário:

2 θ = 80 °

σ x ' = 7,5 + ( - 62,5 ) ⋅ cos ⁡ 80 ° + ( - 35 ) ⋅ s e n ( 80 ° )

σ x ' = - 37,8   M P a

σ y ' = 7,5 - ( - 62,5 ) ⋅ cos ⁡ 80 ° - ( - 35 ) ⋅ s e n ( 80 ° )

σ y ' = 52,8   M P a

τ x y ' = - ( - 62,5 ) ⋅ sen ⁡ 80 ° + ( - 35 ) ⋅ c o s ( 80 ° )

τ x y ' = 55,47   M P a

Passo 5

Para a letra B onde a rotação é de 15° no sentido horário:

2 θ = - 30 °

σ x ' = 7,5 + ( - 62,5 ) ⋅ cos ⁡ - 30 ° + ( - 35 ) ⋅ s e n ( - 30 ° )

σ x ' = - 29,1   M P a

σ y ' = 7,5 - ( - 62,5 ) ⋅ cos ⁡ - 30 ° - ( - 35 ) ⋅ s e n ( - 30 ° )

σ y ' = 44,1   M P a

τ x y ' = - ( - 62,5 ) ⋅ sen ⁡ - 30 ° + ( - 35 ) ⋅ c o s ( - 30 ° )

τ x y ' = - 61,5   M P a

Resposta

a)

σ x ' = - 37,8   M P a

σ y ' = 52,8   M P a

τ x y ' = 55,47   M P a

b)

σ x ' = - 29,1   M P a

σ y ' = 44,1   M P a

τ x y ' = - 61,5   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando o método da sec 7.4 resolver o problema 7.2
Uma barra de aço maciça, de diâmetro d, e é apoiada como mostrado. Sabendo-se que para o aço y= 7,7 x 104 N/m³, determinar o menor diâmetro d que pode ser usado, se a tensão normal não deve exceder 35
Desenhar os diagramas de força cortante e de momento fletor para a viga com o carregamento mostrado e determinar o máximo valor absoluto a) força cortante b) momento fletor.
Determinar: a) Intensidade P de duas forças, dirigidas de baixo para cima, para que o máximo valor absoluto do momento fletor na viga seja tão pequeno quanto possível; b) a correspondente tensão norma
Desenhar os diagramas de força cortante e de momento fletor para a viga com o carregamento mostrado e determinar o máximo valor absoluto a) força cortante b) momento fletor.