Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 127

A esteira transportadora A, que forma um ângulo de 20° com a horizontal, se move a uma velocidade constante de 1,2 m/s e é usada para carregar um avião. Sabendo que um trabalhador joga uma bolsa B com uma velocidade inicial de 0,7 m/s a um ângulo de 30° com a horizontal, determine a velocidade da bolsa em relação à esteira ao cair nessa esteira.

Passo 1

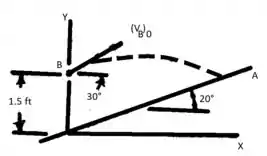Primeiro determine a velocidade da bolsa quando chega na esteira. Agora

[ ( v B ) x ] 0 = ( v B ) 0 c o s 30 °

= ( 1,2 / s ) c o s 30 ° =   1,03   m / s  

[ ( v B ) y ] 0 = ( v B ) 0 s e n 30 °

= ( 1,2   m / s ) s e n 30 ° = 0,6   m / s

Passo 2

Movimento horizontal. (Uniforme)

x = 0 + [ ( v B ) x ] 0 t = ( 2.5 cos ⁡ 30 ° ) t

( v B ) x = [ ( v B ) x ] 0 = 1,2   c o s   30 °

Passo 3

Movimento Vertical. (Movimento Uniformemente Acelerado)

y = y 0 = [ ( v B ) y ] 0 t - 1 2 g t ² = 1.5 + 2.5   s e n   30 ° t - 1 2 g t 2

( v B ) y = ( v B ) y 0 - g t = 2.5   s e n   30 ° - g t

A equação da linha colinear com o topo da superficie da esteira é

y = x tan ⁡ 20 °

Passo 4

Por isso, quando a bolsa chegar na esteira

1.5 + 2.5   s e n   30 ° t - 1 2 g r 2 = [ ( 2.5 cos ⁡ 30 ° ) t ] tan ⁡ 20 °

Ou

1 2 32.2 t 2 + 2.5 ( cos ⁡ 30 ° tan ⁡ 20 ° - s e n   30 ° ) t - 1.5 = 0

16.1 t 2 - 0.46198 t - 1.5 = 0

Resolvendo t=0.31991s e t=-0.29722s ( rejeitado)

A velocidade v B da sacola quando cai na esteira é de

Passo 5

v B = ( 2.5 cos ⁡ 30 ° ) i + 2.5   s e n   30 ° - 32.2 0.31992 j

= ( 2.1651 m / s ) i - ( 9.0514   m / s ) j

Finalmente

v B = v A = v B / A

ou

v B / A = 2.1651 i - 9.0514 j - 4 ( cos ⁡ 20 ° i + s e n   20 ° j )

= - ( 1.59367 m / s ) i - ( 10.4195   m / s ) j

ou

v B / A = 10.54   m / s   ∡ 81.3 °

Resposta

v B / A = 10.54 m / s   ∡ 81.3 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um trem de brinquedo possui acoplamentos magnéticos cuja força de atração máxima é 0,9N entre carros adjacentes. Qual é a força máxima P com a qual uma criança pode puxar a locomotiva e não romper o t
Determine a tração P no cabo que dará ao bloco de 50k g uma aceleração constante de 2m / s 2 para cima no plano inclinado.
O avião comercial a jato A com 340t possui quatro motores, cada um dos quais produz um empuxo quase constante de 200k N durante a decolagem. Uma pequena aeronave B taxia em direção à extremidade da pi
Um pequeno pacote é depositado pela correia transportadora em uma rampa com 30 ° em A com uma velocidade de 0,8m / s . Calcule a distância s sobre a superfície plana B C na qual o pacote atinge o repo
Um pequeno projétil é lançado a partir do ponto O com uma velocidade inicial de u = 500m / s no ângulo de 60 ° em relação à horizontal como mostrado. Despreze a resistência atmosférica e qualquer vari