Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 10

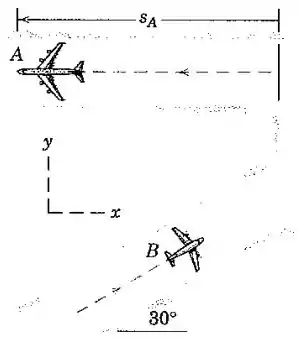
O avião comercial a jato A com 340   t possui quatro motores, cada um dos quais produz um empuxo quase constante de 200   k N durante a decolagem. Uma pequena aeronave B taxia em direção à extremidade da pista com uma velocidade constante v B = 25   k m / h . Determine a velocidade e a aceleração que A aparenta ter em relação a um observador em B 10 segundos após A iniciar a sua decolagem. Despreze a resistência do ar e de rolamento.

Passo 1

Galera, a primeira coisa a se fazer aqui é calcular com que aceleração a x o avião A se move ao longo do eixo x . Para isso, usamos a Segunda Lei de newton:

∑ F x = m a x

4 - 200   k N = 340   t   a x

- 800 10 3   N = 340 10 3   k g   a x

a x = - 2,35   m / s 2

Já aceleração da aeronave B é nula, pois ela se move com velocidade constante. Então, a aceleração relativa será:

a A B = a x - 0

a A B = - 2,35   m / s 2

Ou seja, A aparenta ter uma aceleração de 2,35   m / s 2 para a esquerda e aceleração nula na direção do eixo y :

a A B = - 2,35   i + 0   j   m / s 2

Passo 2

Agora vamos calcular a velocidade de A depois de 10 segundos:

v A x = v 0 + a t = 0 + - 2,35 10

v A x = - 23,5   m / s

Na direção x , a velocidade de B será:

v B x = v B cos ⁡ 30 °

E na direção y :

v B y = v B   s e n   30 °

Lembrando que v B = 25   k m / h = 6,94   m / s , obteremos:

v B x = 6   m / s

v B y = 3,47   m / s

Então, na direção x , a velocidade relativa será:

v A B x = v A x - v B x = - 23,5 - 6

v A B x = - 29,5   m / s

E na direção y :

v A B y = v A y - v B y = 0 - 3,47

v A B y = - 3,47   m / s

Logo, podemos escrever:

v A B = - 29,5   i - 3,47   j   m / s

Resposta

a A B = - 2,35   i + 0   j   m / s 2

v A B = - 29,5   i - 3,47   j   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a velocidade necessária da correia B se a velocidade relativa com a qual a areia atinge a correia B é (a) vertical, (b) a menor possível.
Os aviões A e B estão voando à mesma altitude e acompanhando o olho de um furacão C. A velocidade relativa de C em relação a A é vC/A = 235 km/h 40°. Determine (a) a velocidade relativa de B em relaçã
Um radar costeiro indica que uma barca sai de seu atracadouro com uma velocidade v = 18,5 km/h 70°, enquanto instrumentos a bordo da barca indicam velocidade de 19 km/h e direção 30° a oeste da direçã
À medida que o caminhão mostrado na figura começa a dar ré com uma aceleração constante de 1,2 m/s² , a seção exterior B da sua lança começa a se retrair com uma aceleração constante de 0,5 m/s² relat
Sabendo que no instante mostrado na figura o bloco A tem velocidade de 8 cm/s e aceleração de 6 cm/s² , ambas no sentido de descida da rampa, determine (a) a velocidade do bloco B, (b) a aceleração do