Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 125
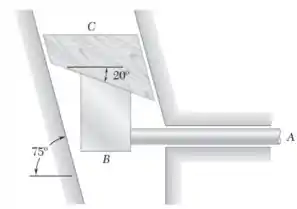
A montagem da barra A com a cunha B sai do repouso e se move para a direita com aceleração constante de 2 mm/s² . Determine (a) a aceleração da cunha C, (b) a velocidade da cunha C quando t 10 s.
Passo 1
(a)Nós temos
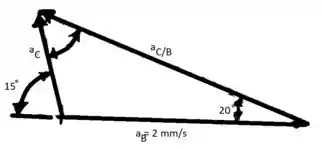
A representação gráfia desse equação é como esta mostrado.
Primeiro note
Então
Passo 2
(b)Para movimento de aceleração uniforme
Em t=10s:
ou
Resposta
Exercícios de Livros Relacionados
Um carro parte do repouso e acelera a uma taxa constante até atingir 100k m / h em uma distância de 60m , momento em que é desengrenado. O carro então diminui para uma velocidade de 50k m / h em uma d
Um projétil de teste é disparado horizontalmente em um líquido viscoso com uma velocidade de v 0 . A força de desaceleração é proporcional ao quadrado da velocidade, de modo que a aceleração torna-se
O motorista de um carro, que está inicialmente em repouso no topo A de uma ladeira, libera os freios e desce em ponto morto com uma aceleração em metros por segundo ao quadrado dada por a = 0,981 - 0,
Com uma boa aproximação a pressão atrás de uma bala de espingarda varia inversamente com a posição do ponto x ao longo do cano. Assim, a aceleração da bala pode ser escrita como a = k / x , onde k é u
Para a bola de beisebol do Prob. 2/51 atirada para cima com uma velocidade inicial de 30m / s , determine o tempo t s do solo até o ápice e o tempo t d do ápice até o solo.Prob. 2/51: Quando o efeito