Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.10 - Ex. 236
Um pequeno projétil é lançado a partir do ponto com uma velocidade inicial de no ângulo de em relação à horizontal como mostrado. Despreze a resistência atmosférica e qualquer variação em e calcule o raio de curvatura da trajetória do projétil segundos após o disparo.
Passo 1
Bom, o segredo pra calcular o raio de curvatura da trajetória é achar o módulo da aceleração normal, que é a componente da aceleração que é normal à trajetória da partícula, e também o módulo da velocidade. Depois que fizermos isso:
Pronto, teremos o raio de curvatura.
Nesse caso, a única aceleração envolvida é a da gravidade, que é sempre vertical para baixo:
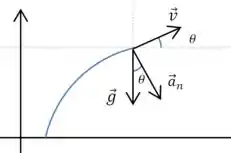
Nós podemos definir esse ângulo como o ângulo que o vetor velocidade faz com a horizontal:
E aí podemos mostrar pelo desenho que esse também é o ângulo que a aceleração normal forma com o vetor ! Ou seja:
Passo 2
Vamos ver onde essas equações nos levam. Isolando na primeira e substituindo na segunda:
E voltando na definição da aceleração normal:
Só que podemos escrever o em função de e :
Ou seja, só o que precisamos para resolver esse problema é achar os componentes e da velocidade do projétil no instante de tempo que foi pedido.
Passo 3
Por sorte o enunciado já deu tudo o que precisamos para calcular isso. Como não existe aceleração na direção horizontal:
Então, no instante :
Agora voltando na nossa fórmula:
E agora é só jogar na calculadora:
Pronto!
Resposta
O raio de curvatura é .