Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.3 - Ex. 46
Estime a força necessária para levantar do chão os pneus traseiros do carro de corrida. Você pode assumir que a parte do macaco é horizontal. A massa combinada do carro e do motorista é com centro de massa em . O motorista pisa nos freios durante o levantamento. Apresente quaisquer suposições adicionais.
Passo 1
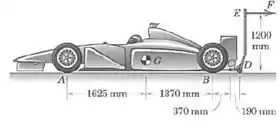
Vamos começar desenhando as forças que atuam sobre o carro (ou seja, ignorando o macaco por enquanto).
Como o macaco está empurrando a traseira do carro para cima, temos uma força normal atuando na roda , e outra atuando no ponto por onde o carro é suspenso. Além dessas duas forças, temos o peso e a força que mantém o contato entre o macaco e o carro:
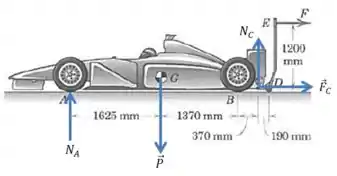
Vamos procurar alguma equação de equilíbrio para esse carro. Se pensarmos no limite em que a roda traseira começa a se erguer, podemos escrever o seguinte:
E escolhemos o ponto por conveniência, para que a força suma da equação:
Ótimo, já encontramos uma das forças que agem sobre o macaco.
É importante notar que a força não tem momento exatamente nulo, porque ela está um pouco acima da altura do ponto , mas podemos desconsiderar isso.
Passo 2
Agora vamos olhar apenas para o macaco:
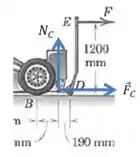
E podemos usar uma equação de equilíbrio parecida com a que usamos no passo :
Já que estamos considerando o equilíbrio das forças no limite, quando a roda traseira está prestes a se erguer.
Como a linha de ação da força cruza o ponto (já que a linha é horizontal, segundo o enunciado), ela não produz momento, então temos apenas o seguinte:
Pronto!
Resposta
A força necessária é .