Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 6.Problemas - Ex. 93
O cortador de tudo é preso em volta do tubo . Se a roda em exerce uma força normal sobre o tubo, determine as forças normais das rodas e sobre o tubo. As três rodas possuem um raio de e o tubo tem um raio externo de .
Passo 1
Para encontrarmos as forças normais em e em tomemos o seguinte diagrama de forças
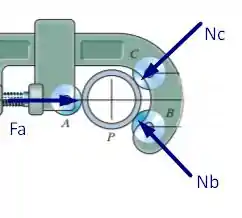
Além disso, admitimos que . Então, tomando as equações de equilíbrio vamos ter
Resposta
Exercícios de Livros Relacionados
Um braço oscilante com roletes em A e B é mostrado na posição em que a válvula está aberta e a mola da válvula está totalmente comprimida. Nessa posição, a força na mola vale 900N . Determine a força
O pequeno barco a vela pode ser inclinado quando preso às docas, como mostrado, para se realizar reparos abaixo da linha d’água. Uma corda é passada sobre a quilha e presa à doca. Outra corda é presa
Um torque de 24Nm é necessário para girar o parafuso em torno de seu eixo. Determine P e as forças entre as paredes endurecidas e lisas da chave e os vértices A e B da cabeça hexagonal do parafuso. Co
Uma parte do mecanismo de troca de marcha para um carro com transmissão manual está mostrada na figura. Para a força de 8N exercida na alavanca de câmbio, determine a força P correspondente exercida p
Estime a força F necessária para levantar do chão os pneus traseiros do carro de corrida. Você pode assumir que a parte C D do macaco é horizontal. A massa combinada do carro e do motorista é 700k g c