Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 3.Problemas - Ex. 28
3.28. Duas esferas, A e B, tem massas iguais e estão eletrostaticamente carregadas, de modo que a força repulsiva que atua entre elas tem uma intensidade de e está direcionada ao longo da linha AB. Determine o ângulo , a tração nas cordas AC e BC e a massa de cada esfera.
Passo 1
Falaa! Ele quer a tração nas cordas, e massa das esferas. Não se assusta com essa história de eletrostática, isso é só para dizer que há duas forças agindo, uma em cada esfera, no sentido e direção mostrados.
Vamos começar desenhando o diagrama de corpo livre para B:
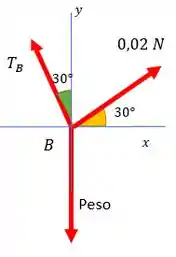
Então vamos ficar com as seguintes equações de equilíbrio
Para x
O que nos leva
Então
Agora o eixo y
O que nos leva
Aí para achar a massa é só dividir o peso pela gravidade:
Passo 2
Agora vamos fazer o mesmo para o ponto A
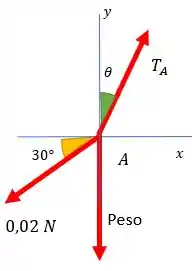
Para x
O que nos leva
Agora o eixo y
O que nos leva
Para determinar vamos fazer
Então
Passo 3
Agora podemos determinar