Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 3.Problemas - Ex. 23

3.23. Determine o comprimento não deformado da mola AC se uma força P = 400   N torna o ângulo θ = 60 ° para o equilíbrio. A corda AB tem 0,6   m de extensão. Considere k = 850 N m .

Passo 1

Vamos começar calculando o comprimento AB, que é a mola deformada, vamos chamar esse comprimento de l

Então

l = 1,2 2 + 0,6 2 - 2 ⋅ 1,2 ⋅ 0,6 ⋅ cos ⁡ 60 °

Fazendo todos os cálculos

l ≈ 1,04

Passo 2

Agora vamos usar a lei dos senos para determinar ϕ

1,04 sin ⁡ 60 ° = 0,6 sin ⁡ ϕ

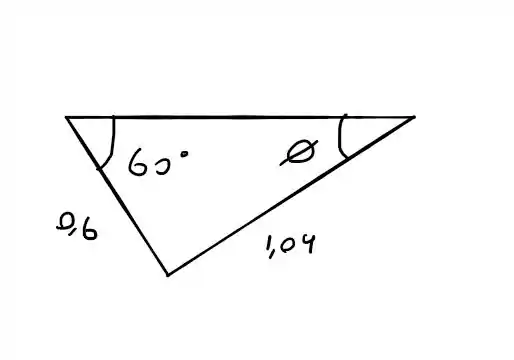
Então

ϕ = s i n - 1 0,6 1,04 ⋅ sin ⁡ 60 ° = 30 °

Passo 3

Agora finalmente podemos usar as equações de equilíbrio

F R y = 0

F R y = T ⋅ sin ⁡ 60 ° + F k ⋅ sin ⁡ 30 ° - 400 = 0

T ⋅ sin ⁡ 60 ° + F k ⋅ sin ⁡ 30 ° = 400     ( 1 )

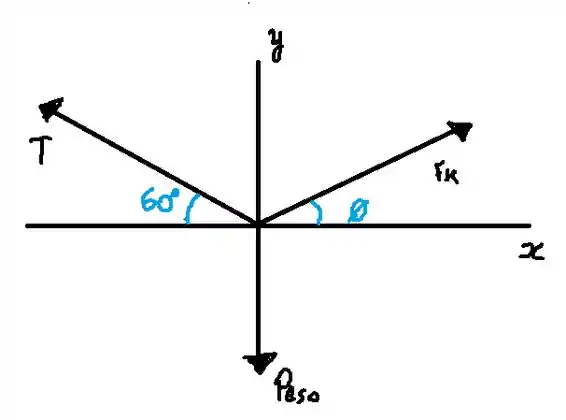
E

F R x = 0

F R x = - T ⋅ cos ⁡ 60 ° + F k ⋅ cos ⁡ 30 ° = 0

F k ⋅ cos ⁡ 30 ° = T ⋅ cos ⁡ 60 °   ( 2 )

Para achar o comprimento da mola não deformada o melhor a fazer é determinar F k , então vamos fazer isso

De (2) temos

F k ⋅ cos ⁡ 30 ° cos ⁡ 60 ° = T

Substituindo em (1)

F k ⋅ cos ⁡ 30 ° cos ⁡ 60 ° ⋅ sin ⁡ 60 ° + F k ⋅ sin ⁡ 30 ° = 400  

F k ⋅ cos ⁡ 30 ° ⋅ tan ⁡ 60 ° + sin ⁡ 30 ° = 400  

Ficamos com

F k = 400 cos ⁡ 30 ° ⋅ tan ⁡ 60 ° + sin ⁡ 30 ° = 200   N

Passo 4

Sabemos que

F k = k ⋅ x

Onde x é o tamanho da mola l menos o tamanho da mola relaxada l ' , que é o que queremos encontrar

Então

F k = k ⋅ l - l '

Vamos isolar l '

l ' = l - F k k

Então

l ' = 1,04 - 200 850 ≈ 0,8   m

Resposta

l ' = 0,8   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O homem empurra o cortador de grama a uma velocidade constante, com uma força P que é paralela ao plano inclinado. A massa do cortador, com o saco de grama preso a ele, é de 50k g e tem centro de mass
Se o bloco de 5k g é suspenso pela polia B e a curvatura da corda é d = 0,15m , determine a força na corda ABC. Despreze a dimensão da polia.
A viga tem um peso de 3,5 kN. Determine o cabo mais curto ABC que pode ser usado para levantá-la se a força máxima que o cabo pode suportar é 7,5k N .
Exercício de Livro
Se a massa do cilindro C é 40 kg, determine a massa do cilindro A, de modo a manter a montagem na posição mostrada.