Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.3 - Ex. 60
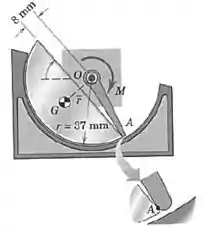
Alguns elementos do sistema de fazer gelo de um refrigerador estão mostrados na figura. (Um “cubo” tem a forma de um segmento cilíndrico!) Uma vez que o cubo congela e um pequeno aquecedor (não mostrado) forma um filme fino de água entre o cubo e superfície de apoio, um motor gira o braço ejetor para remover o cubo. Se existem oito cubos e oito braços, determine o torque necessário em função de . A massa dos oitos cubos é e a distância do centro de massa . Despreze o atrito e assuma que a resultante da força normal distribuída atuando sobre o cubo passa pelo ponto .
Passo 1
Vamos começar escrevendo uma equação de equilíbrio para o cubo de gelo:
Temos duas forças produzindo momento aqui: a componente do peso, e a força de contato do “ponteiro” no ponto .
Como a posição do ponto de ação da força peso é a distância do centro de massa, e a da força de contato é o próprio raio do ponteiro:
Passo 2
Agora vamos usar a mesma equação de equilíbrio para o “ponteiro”:
Nesse caso, além do momento que está representado na figura, temos o momento da força que atua no ponto , e que acabamos de calcular.
Resolvido! Lembrando que o enunciado pediu a resposta em termos de .
Resposta
O torque necessário é .