Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 148
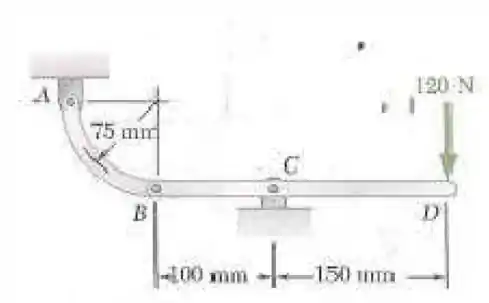
Para a estrutura e carregamento mostrado na figura, determine as reações em A e C.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Precisamos determinar as reações em A e C .
Olhando para a imagem do enunciado, podemos notar que todas as forças estão em (Newtons) e todas as medidas em mm (milímetros). Portanto não precisaremos fazer conversçoes.
Passo 2
A estrutura é composta por dois elementos unidos por um pino em B. Consideraremos os dois elementos separadamente. O primeiro elemento (AB) possui reações apenas em A e B, dessa maneira, o valor das forças A e B devem ser iguais, atuarem na mesma direção e em sentidos opostos para manter o equilíbrio. Pela geometria do elemento vemos que essas forças estão orientadas com um ângulo de 45°, conforme demonstrado no diagrama abaixo, que apresenta a distribuição das forças no elemento AB.
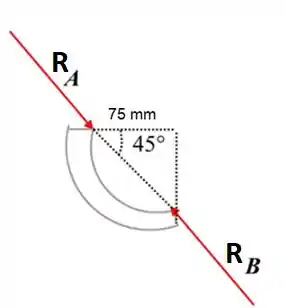
No componente BD a reação em B aparece com mesmo valor e direção (45°) com relação ao componente AB só que com sentido oposto. O que assegura isso é a lei da ação e reação.
Passo 3
Abaixo é apresentado um diagrama de corpo livre desse elemento:
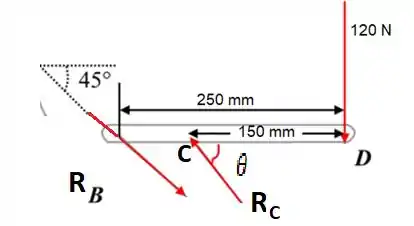
Aplicando o somatório dos dos momentos em torno de C, poderemos encontrar a reação .
=0
Passo 4
Aplicaremos o somatório das forças verticais e das forças horizontais para determinar as componentes de da reação em C
O sinal positivo em ambos os componentes mostra que o sentido da força é o mostrado no diagrama, com orientação no segundo quadrante. Agora determinaremos o módulo da reação e o ângulo