Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 175

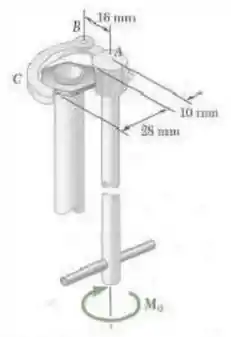
A chave inglesa especial para encanadores mostrada na figura é utilizada em espaços exíguos (por exemplo, sob um lavatório ou pia). Consiste essencialmente em um mordente B C articulado em B a uma haste longa. Sabendo que as forças exercidas sobre a porca são equivalentes a um binário no sentido horário (quando visto de cima) de momento 13.5   N ⋅ m , determine a a intensidade da força exercida pelo pino B no mordente B C , b o binário M 0 aplicado à chave.

Passo 1

Primeiramente, para encontrarmos a força exercida pelo pino B no mordente B C devemos reparar que B C é um membro de duas forças e, assim, podemos fazer a seguinte proporção entre as forças

C y 38 m m = C x 16 m m → C y = 2.375 C x

Das condições de equilíbrio de um corpo tiramos que

∑ F x = 0 → B x = C x

∑ F y = 0 → B y = C y = 2.375 C x

Para a porca vamos ter

∑ F x = 0 → C x = D x

∑ M = 13.5 N ⋅ m → C x ⋅ 0.28 m = 13.5 N ⋅ m → C x = 48.21 N

Passo 2

Obtido o valor de C x conseguimos calcular o valor de C y ,   B y   ,   B x   e   D x obtendo os seguintes valores

C y = B y ≈ 114.51 N

C x = D x = B x = 48.21 N

Assim, teremos que o valor de B é dado por

B = B x 2 + B y 2 = 114.51 2 + 48.21 2 = 124.24 N

Passo 3

Por fim, para descobrirmos o valor de M 0 apliquemos as condições de equilíbrio para a porca e obteremos, então,

∑ M d = 0 →   - M 0 + B y ⋅ 0.16 m - B x ⋅ 0.1 m = 0

M 0 = 114.51 N ⋅ 0.16 m - 48.21 N ⋅ 0.1 m

M 0 = 13.5 N ⋅ m

Resposta

a   124.24 N

b M 0 = 13.5 N ⋅ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O anteparo A D está sujeito às pressões da água e do aterramento de contenção. Supondo que A D esteja conectado ao solo em A por um pino, determine as reações horizontal e vertical nesse ponto e també
A lança deverá apoiar duas cargas verticais, F 1 e F 2 . Se o cabo C B pode sustentar uma carga máxima de 1500 N antes de se romper, determine as cargas críticas se F 1 = 2 F 2 . Além disso, qual é a
Determine a rigidez k de cada mola de modo que a força de 30 N faça com que o elemento sem peso se incline de θ = 15 ° quando a força é aplicada. Originalmente, o elemento está horizontal e as molas n
Um elemento horizontal de peso desprezível é apoiado por duas molas, cada uma com rigidez k = 100N / m . Se as molas estiverem inicialmente não esticadas e a força for vertical, conforme mostrado, det
O tubo liso é encostado na abertura, nos pontos de contato A , B e C . Determine as reações nesses pontos, necessárias para suportar a força de 300N . Para o cálculo, desconsidere a espessura do tubo.