Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 97
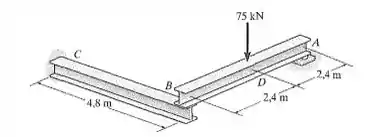
A estrutura é composta por uma viga em balanço CB e uma viga simplesmente apoiada AB. Se cada uma for feita de aço A-36 e tiver momento de inércia em torno de seu eixo principal , determine o deslocamento no centro D da viga BA.
Passo 1
Fala aí galera, partiu resolver outra questão de resmat. Sabemos que a engenharia ama tabelas, logo, os procedimentos feitos até agora, aquelas integrais malucas, estão todos tabelados. Essa seção do livro nos faz trabalhar com as tabelas, para utilizar as fórmulas. Obviamente, essas fórmulas são geralmente dadas quando a questão quer que a gente utilize.
Logo, a fórmula para este caso será:
Sabemos, pela tabela, que:
Substituindo os valores, teremos:
Resposta
Exercícios de Livros Relacionados
Determine as reações nos apoios de mancal A , B e C do eixo; a seguir, trace os diagramas de força cortante e momento fletor. E I é constante. Cada mancal exerce somente reações verticais sobre o eixo
Determine as reações em A e B . Considere que o apoio em A exerce somente um momento sobre a viga. E I é constante.
Determine a reação nos apoio C . E I é constante para ambas as vigas.
Determine as reações nos apoios A , B e C ; a seguir, trace os diagramas de força cortante e momento fletor. E I é constante.
A viga é feita de um material elástico macio com EI constante. Se ela estiver originalmente à distância ∆ da superfície do apoio de sua extremidade, determine a distância a à qual a extremidade da vig