Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 37

O mancal de encosto está sujeito às cargas mostradas. Determine a tensão normal média desenvolvida nas seções transversais que passam pelos pontos B, C e D. Faça um rascunho dos resultados sobre um elemento de volume infinitesimal localizados em cada seção.

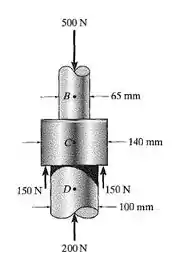
Passo 1

Primeiramente, faremos cortes nas seções para determinar as forças atuantes nos trechos.

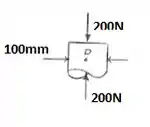
Portanto, sabemos que as forças atuantes em D, C e B são, respectivamente, 200N, 500N e 500N.

Passo 2

O próximo passo é calcularmos as áreas das seções transversais com os diâmetros fornecidos.

A d = π 100 ² 4 = 7853,75

A c = π 140 2 4 = 15393,35

A b = π 65 ² 4 =3318,2

Passo 3

Com as áreas e as forças atuantes nas seções, podemos calcular a tensão normal destas.

σ d = 200 7853,75 = 25,5 K P a

σ c = 500 15393,35 = 32,5 K P a

σ b = 500 3318,2 = 151 K P a

Observe que os resultados foram arredondados.

O problema nos pede uma representação dos elementos infinitesimais, os quais estão mostrados abaixo:

Resposta

σ d = 200 7853,75 = 25,5 K P a

σ c = 500 15393,35 = 32,5 K P a

σ b = 500 3318,2 = 151 K P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas barras cilíndricas maciças são ligadas em B e carregadas como mostrado. A barra A B é de aço ( E = 200G P a ) e a barra B C é de latão ( E = 105G P a ) . Determinar: ( a ) a deformação total da b
Uma coluna de concreto de 1,2 m de altura é reforçada por quatro barras de aço, cada uma com 20 m m de diâmetro. Sabendo-se que os módulos de elasticidade para o concreto e aço são 25 M P a e 200 M P
Resolver o problema 2.16 , considerando que o tubo é de latão ( E = 415G P a ) e a barra de alumíno ( E = 70G P a ).
Um tubo de alumínio de 250m m de comprimento ( E = 70G P a ) , e com diâmetro externo de 36m m e interno de 28m m , pode ser fechado em ambas as extremidades por meio de tampas com roscas simples, de
A carga axial na coluna, que sustenta a viga de madeira mostrada, é de 100k N . Determine o comprimento l da placa de apoio para que a tensão de esmagamento média na madeira seja de 2,8M P a .