Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 24
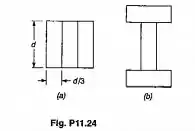
Uma coluna de comprimento efetivo L pode ser confeccionada pregando-se firmemente as pranchas idênticas, tal como mostrado. Para a espessura das pranchas indicadas, determinar a razão entre a carga crítica usando o arranjo a, e a carga crítica usando o arranjo b.
Passo 1
Fala meu povo, bora resolver rapidinho essa aqui?
Bom o enunciado nos pede a razão entre as cargas críticas dos arranjos de forma que eles tenham o mesmo material e mesmo comprimento efetivo. Bora dar uma olhada na fórmula da carga crítica.
Repare que nessas condições a única coisa que vai ser diferente é o momento de inércia!
Então podemos dizer que:
Nossa meta então é calcular os momentos de inércia e resolver essa parada!
Passo 2
O momento de inércia da disposição a é simples, com as pranchas unidas temos uma seção do tipo quadrada maciça.
Para a seção composta vale a gente analisar melhor:
Esse tipo de seção I, tem o momento de inércia que pode ser encontrado calculando o momento de inércia das partes separadas.
Muita atenção aqui, esse tipo de peça possui um eixo mais fraco, normalmente calcula se para os dois casos e avalia-se o eixo mais fraco mas para seções do tipo I o eixo fraco é o eixo y pois é em torno desse eixo que a peça possui maior chance de girar.
Substituindo esses valores na fórmula mostrada para o cálculo do momento de inércia da seção temos:
Rearrumando isso com nossa bela regra de frações de repetir o primeiro e multiplicar pelo inverso do segundo temos: