Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 92
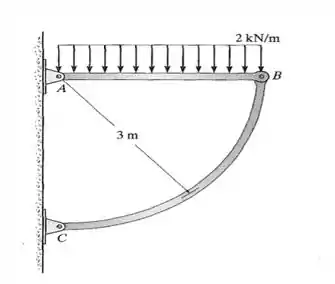
A estrutura está sujeita ao carregamento distribuído de . Determine o diâmetro exigido para os pinos em e se a tensão de cisalhamento admissível para o material for . Ambos os pinos estão sujeitos a cisalhamento duplo.
Passo 1
Falaaaa! Queremos dimensionar o diâmetro dos pinos, então precisamos começar achando os esforços sobre eles.
Mas repara que eles estão nos apoios do elemento . Então as reações nos apoios já vão ser esses esforços sobre os pinos. Aí só precisamos achá-las!
Olha esse
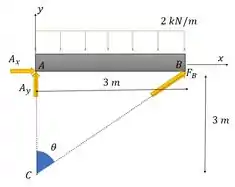
Como queremos dimensionar o diâmetro exigido pelos pinos e devemos perceber que o membro está sujeito a atuação de duas forças, e , além disso, para facilitar as contas vamos definir como orientação e .
Bora!
Passo 2
Primeiramente, vamos encontrar as reações dos suportes obtendo o seguinte
Considerando o sentido anti-horário como positivo
A resultante da força em dada por pode ser calculada como
Repara que , então os esforços nos dois pinos são iguais.
Passo 3
Lembrando que a tensão de cisalhamento é dada por
Substituindo os valores encontrados acima vamos obter
Sendo , por causa do cisalhamento duplo:
Como a gente quer o diâmetro mínimo, a gente substitui essa tensão média pela tensão admissível:
Passo 4
Aí gente lembra que os dois pinos estão sujeitos a esforços iguais, ou seja, iguais. E tem tensões admissíveis iguais. Então, eles vão ter o mesmo diâmetro! (já que a expressão do diâmetro depende dessas duas grandezas.
Substituindo os valores na expressão que a gente achou, vamos obter