Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 101
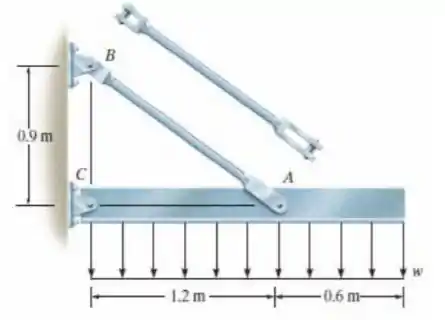
O conjunto de pendural é usado para suportar um carregamento distribuído . Determine a tensão de cisalhamento média no parafuso de de diâmetro em e a tensão de tração média na haste , com diâmetro de . Se a tensão de escoamento por cisalhamento para o parafuso for e a tensão de escoamento por tração para a haste for , determine o fator de segurança em relação ao escoamento em cada caso.
Passo 1
E aí meu povo, tudo joia com vocês? Espero que estejam bem e preparados para mais uma resolução bacaninha. A gente quer achar a tensão média em , e no pino . E saber o fator de segurança dessas tensões.
Antes de tudo, vamos deixar anotado aqui os dados fornecidos pelo enunciado e coloca-los de acordo com a notação que adotaremos aqui, então
E temos também o diâmetro do pino e da barra AB:
Devemos observar que a força que atua sobre a barra na horizontal pode ser decomposta em uma componente horizontal e uma componente vertical da seguinte forma
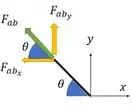
A gente sabe que ela precisa estar nesse sentido porque ela é responsável por segurar o elemento com a carga distribuída. E aí a gente pode escrever as componentes dela assim:
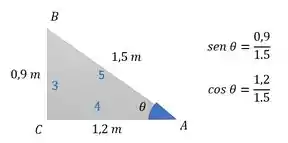
Esse seno e cosseno a gente escrever usando a trigonometria do triângulo de catetos e . Percebe que ele é do tipo 3/4/5, porque se a gente divide esses catetos por , a gente acha e . Logo teremos algo assim:
Passo 2
Agora que fizemos toda nossa base para a resolução, vamos a ela. Como a gente quer a tensão em e no pino , precisamos descobrir .
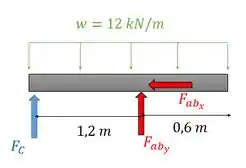
Para isso, vamos calcular o somatório de momento em , tendo o sentido anti-horário como positivo, assim, a gente ignora , e acha só que a gente quer ehehe
Substituindo nossa expressão de e de :
Isolando :
Passo 3
Dessa forma, temos tudo o que é necessário para calcularmos as tensões. Vamos começar com a tensão de cisalhamento média no parafuso que vai ser dada por
Percebe pelo detalhe do parafuso que ele é ligado na barra por uma placa. E na por duas. Isso faz com que a gente tenha uma situação assim:
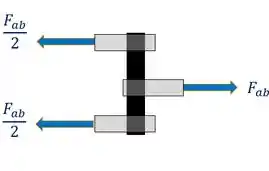
Onde a força na barra é transmitida para a barra através de duas placas, que recebem metade dessa força cada uma. Aí nessa situação, dizemos que o cisalhamento é duplo e . Assim nossa expressão da tensão fica:
E como o parafuso tem seção circular:
Passo 4
Substituindo os dados:
O resultado sai em porque a gente usou e (newtons).
E o fator de segurança dessa tensão em relação ao escoamento é calculado assim
Ou seja, o fator de segurança de uma tensão é sempre a razão entre a tensão admissível de e a tensão que de fato o elemento suporta. Substituindo os dados:
Passo 5
Vamos lá, já estamos quase acabando e se você chegou até aqui não vamos desistir agora, né? Lembre-se: o Naruto não desistiria. Pois então, para a haste nós temos que a força de tração média será dada por
Onde e o diâmetro a ser usado vai ser , dessa forma vamos obter
Agora o gran finale para acabar com o problema de vez vamos ter que o fator de segurança para a haste será
Novamente o é dado pela razão entre tensão admissível e tensão suportada na situação. Substituindo os valores: