Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 2.Problemas - Ex. 132
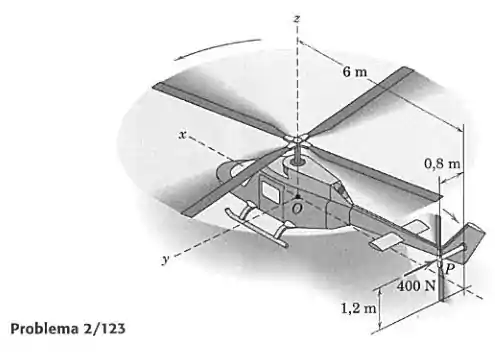
Eum helicóptero está mostrado e são dadas certas coordenadas tridimensionais. Durante um teste no solo, uma força aerodinâmica de 400 N é aplicada ao rotor da cauda em , como mostrado. Determine o momento desta força em relação ao ponto na fuselagem.
Passo 1
Vamos calcular o momento pelo enfoque vetorialda seguinte maneira:
Então achamos o vetor que vai de P a O e fazemos o priduto vetorial.
Passo 2
As coordenadas do ponto são:
Então o vetor é:
E a força é
Passo 3
Nosso produto vetorial é então:
Colocamos na forma de determinante:
Resolvendo o determinante, encontramos o valor:
Resposta
Exercícios de Livros Relacionados
57. Determine a intensidade do momento que a força F → exerce sobre o eixo y da manivela. Resolva o problema usando uma abordagem de vetor cartesiano e usando uma abordagem escalar.
54. Determine a intensidade dos momentos da força F → em relação aos eixos x, y e z. Resolva o problema (a) usando uma abordagem de vetor cartesiano
A tubulação é fixa na parede pelas duas abraçadeiras. Se o vaso de planta possui um peso 250N , determine a intensidade do momento produzido pelo peso em relação ao eixo O A .
64. A estrutura na forma de um A está sendo suspensa para uma posição ereta pela força vertical F = 400N . Determine o momento dessa força em relação ao eixo x quando a estrutura está na posição mostr
61.Se a tração no cabo é F = 700N , determine a intensidade do momento produzido pela força em relação ao eixo da dobradiça, CD, necessária para manter o painel na posição mostrada.