Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 2.Problemas - Ex. 153
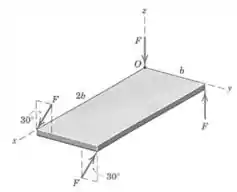
A placa retangular fina está submetida às quatro forças mostradas. Determine o sistema força-binário equivalente em . Qual é a resultante do sistema?
Passo 1
Vamos começar escrevendo formas vetoriais para todas as forças. Começando pela que age sobre o ponto , e depois percorrendo o retângulo no sentido horário:
Dá pra ver que as forças formam dois pares exatamente opostos, então a força resultante vai se anular:
Passo 2
Então nosso sistema força-binário vai incluir apenas um momento gerado por essas forças.
Como temos dois pares de forças com módulos e direções iguais, mas sentidos opostos, podemos calcular os momentos usando a seguinte fórmula:
Que vale para binários de força. Onde é o vetor posição que une os pontos onde as forças são aplicadas, e é o vetor de uma das forças.
Passo 3
Começamos pelo par de forças que agem sobre o eixo :
O vetor posição vai do ponto de aplicação da força até a o da (poderia ser o contrário se usássemos para calcular o momento).
E como o produto vetorial dos vetores unitários é (use a regra da mão direita!):
Passo 4
Agora faremos a mesma coisa para o outro par de forças.
O vetor é igual ao que usamos ali em cima, afinal de contas estamos usando lados simétricos de um retângulo:
Vamos usar a propriedade distribuitiva:
E usando a regra da mão direita vemos que e :
E agora já podemos calcular o momento total:
Resposta
O sistema força-binário é composto por e .