Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 4.Problemas - Ex. 94

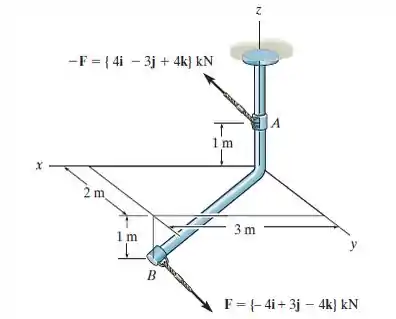
Expresse o momento de binário que age sobre o elemento na forma de vetor cartesiano. Qual é a intensidade do momento de binário?

Passo 1

E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!

Precisamos determinar o momento de binário na sua forma vetorial e depois calcular a intensidade.

Esta é uma questão que precisamos trabalhar com a definição vetorial. Sabemos que o momento é calculado por:

M = r × F

Sendo r a distância do ponto de aplicação a força.

Mas qual a distância vamos escolher???? O ponto A ? O ponto B ? O ponto médio? Um ponto genérico qualquer?

Bom, qualquer um deles serve. Entretanto, existem dois que pontos que facilitam bastante: o ponto A e o ponto B . Eles facilitam bastante pois o momento de binário é igual ao momento da força localizada no outro ponto (se fixarmos a origem no ponto A , basta calcular o momento relativo ao ponto B ).

Passo 2

Agora que já sabemos o que devemos fazer, vamos para os cálculos! Fixando a origem no ponto A , a distância até o ponto B , na forma vetorial, é:

r = 3 i → + 2 j → - 2 k → m

E o momento será:

M = r × F

M = i → j → k → 3 2 - 2 - 4 3 - 4 = - 2 i → + 20 j → + 17 k → k N ⋅ m

E a intensidade do momento é:

M = - 2 2 + 20 2 + 17 2 = 26 , 3   k N ⋅ m

Resposta

M = - 2 i → + 20 j → + 17 k → k N ⋅ m

E a intensidade do momento é:

M = 26,3   k N ⋅ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um computador de 25k g e uma impressora a laser de 10k g estão sobre o tampo horizontal de uma mesa. Determine a resultante do sistema dos dois pesos correspondentes e especifique as coordenadas do po
Substitua as duas forças atuando no mastro por um torçor. Escreva na forma vetorial o momento M → associado com o torçor e especifique as coordenadas do ponto P no plano y - z pelo qual passa a linha
Ao apertar um parafuso cujo centro está no ponto O , uma pessoa exerce, com a mão direita, uma força de 180N no manete da chave de catraca. Além disso, com a mão esquerda exerce uma força de 90N , com
Represente por uma única força R → , em A e por um momento M → a resulatnte do sistema de forças atuando em um conjunto de tubos.
O motor montado na cantoneira suporta seu peso de 160N e seu eixo resiste ao empuxo de 120N e ao torque de 25N m aplicados. Determine a resultante do sistema de forças mostrado em termos de uma força