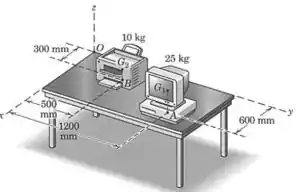
Um computador de e uma impressora a laser de estão sobre o tampo horizontal de uma mesa. Determine a resultante do sistema dos dois pesos correspondentes e especifique as coordenadas do ponto , no plano -, pelo qual passa a resultante. Os dois pesos atuam os pontos e .

Agora vamos calcular os momentos gerados pelos dois pesos, é importante dar uma olhada na imagem do enunciado para entender como escrevemos os vetores e :

E podemos usar a regra da mão direita para resolver os dois produtos vetoriais:

E então, usando a propriedade distributiva:

Agora vamos procurar as coordenadas no plano - pelas quais a força resultante passa. Temos que escolher essas coordenadas de forma que o momento gerado por essa força resultante seja igual ao que acabamos de calcular:

E vamos usar a regra da mão direita mais uma vez:

E então:

Agora ficamos com duas equações:

Resolvendo essas equações encontramos o seguinte: